Direct and Inverse Variations ICSE Class-8th Concise Selina Mathematics Solutions Chapter-10 . We provide step by step Solutions of Exercise / lesson-10 Direct and Inverse Variations for ICSE Class-8 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-10 A, Exe-10 B, Exe-10 C, Exe-10 D and Exe-10 E to develop skill and confidence . Visit official Website CISCE for detail information about ICSE Board Class-8.
Direct and Inverse Variations ICSE Class-8th Concise Selina Mathematics Solutions Chapter-10
–: Select Topics :–
Exercise – 10 A Direct and Inverse Variations
Question 1 :-
In which of the following tables, x and y vary directly:

Answer:
(i)
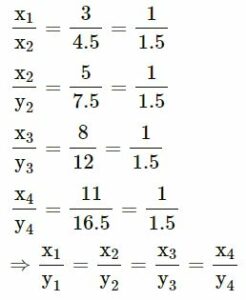
Yes, x and y vary directly.
(ii)
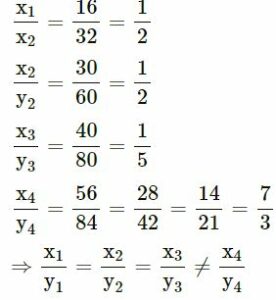
x and y are not in direct variation.

x and y are not in direct variation.
Question 2 :-
If x and y vary directly, find the values of x, y and z:

Answer
x and y are in direct variation

⇒ x = 5, y = 8, z = 120
| x | 3 | 5 | 8 | 10 |
| y | 36 | 60 | 96 | 120 |
Question 3 :-
A truck consumes 28 litres of diesel for moving through a distance of 448 km. How much distance will it cover in 64 litres of diesel?
Answer
et the truck cover x in 64 litres of diesel.
| Diesel (in litres) | 28 | 64 |
| Distance (in km) | 448 | x |
It is the case of direct variation
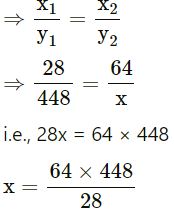
= 1024 km
Question 4 :-
For 100 km, a taxi charges ₹ 1,800. How much will it charge for a journey of 120 km?
Answer
Let a charge of a car is ₹ x in 120 km
| Distance in(km) | 1800 | x |
| Taxi charges (₹) | 100 | 120 |
Since it is the case of direct variation
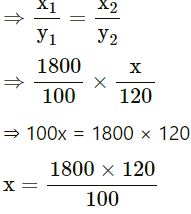
Question 5 :-
If 27 identical articles cost ₹ 1,890, how many articles can be bought for ₹ 1,750?
Answer :
Let x number of articles be purchased in ₹1750
| Cost (₹) | 1890 | 1750 |
| No. of articles | 27 | x |
Since it is a case of direct variation
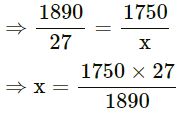
= 25 articles
Question 6 :-
7 kg of rice costs ₹ 1,120. How much rice can be bought for ₹ 3,680?
Answer
Rice: Cost:: Rice: Cost
7 kg : ₹1120 :: x kg : ₹3680
∴ x =7×3680/1120
= 23 kg
Question 7 :-
6 note-books cost ₹ 156, find the cost of 54 such note-books.
Answer:
Notebooks: Cost:: Notebooks: Cost
6 : ₹ 156 :: 54 : ₹ x
∴ x = 156×54/6
= ₹ 1404
Question 8 :-
22 men can dig a 27 m long trench in one day. How many men should be employed for digging 135 m long trench of the same type in one day?
Answer:
Men: Length trench:: Men : Length of trench
22 : 27 m :: x : 135 m
x = 22×135/27
= 110 men
Question 9 :-
If the total weight of 11 identical articles is 77 kg, how many articles of the same type would weigh 224 kg?
Answer:
No. of articles: Weight:: No. of articles: Weight
11 : 77 kg :: x : 224 kg
x = 11×224/77
= 32 articles
Question 10 :-
A train is moving with uniform speed of 120 km per hour.
(i) How far will it travel in 36 minutes?
(ii) In how much time will it cover 210 km?
Answer:
(i) Speed of train in 60 minutes = 120 km
i.e. distance covered in 60 minutes =120/60
Distance covered in 36 minutes =(120×36)/60
= 2 × 36
= 72 km
(ii) If distance covered is 120 km then the time is taken = 60 minutes
If distance covered is 1 km then the time is taken =60/120
If the distance covered is 210 km then the time is taken =(60/120)×210 = 105 minutes
= 1 hours 45 minutes
Exercise – 10 B ICSE Class-8th Concise Selina Mathematics
Question 1 :-
Check whether x and y vary inversely or not.

Answer
(i)
xy = 4 x 6 = 24
xy = 3 x 8 = 24
xy = 12 x 2 = 24
xy = 1 x 24 = 24
xy are equal.
x and y are inversely proportional
(ii)
xy = 30 x 60 = 1800
xy= 120 x 30 = 3600
xy = 60 x 30= 1800
xy = 24 x 75 = 1800
xy are not equal.
x and y are not inversely proportional.
(iii)
xy = 10 x 90 = 900
= 30 x 30 = 900
= 60 x 20= 1200
= 10 x 90 = 900
xy are not equal.
x and y are not inversely proportional.
Question 2 :-
If x and y vary inversely, find the values of l, m and n :

Answer
(i)
∵ x and y are inversely proportional
∴ xy is equal
Now,
xy = 4 × 4 = 16
8 × l = 16 ⇒ l = 16/8 = 2
2 × m = 16 ⇒ m =16/2 = 8
32 × n = 16 ⇒ n = 16/32 = 0.5
(ii)
∵ x and y are inversely proportional
∴ xy is equal
Now,
xy = 32 × 12 = 384
24 × l = 384 ⇒ l = 384/24 = 16
m × 8 = 384 ⇒ m =384/8 = 48
16 × n = 384 ⇒ n = 384/16 = 24
Question 3 :-
36 men can do a piece of work in 7 days. How many men will do the same work in 42 days?
Answer
Men: Days:: Men: Days
36 : 7 :: x : 42
∴ By inverse proportional
36 × 7 = x × 42
⇒ x=(36×7)/42
= 6 men
Question 4 :-
12 pipes, all of the same size, fill a tank in 42 minutes. How long will it take to fill the same tank, if 21 pipes of the same size are used?
Answer
Pipes: Time:: Pipes: Time
12 : 2x :: 21 : 42
∴ By inverse proportion
12 × 42 = 21 × x
⇒ x =(12 × 42)/21
= 24 minutes
Question 5 :-
In a fort 150 men had provisions for 45 days. After 10 days, 25 men left the fort. How long would the food last at the same rate?
Answer
After 10 days :
For 150 men, provision will last (45 − 10)
days = 35 days
⇒ For 1 man, the provisions will last
= 150 × 35 days
And for (150 − 25) = 125 men, the provisions
will last for =(150×35)/125
= 42 days
Question 6 :-
72 men do a piece of work in 25 days. In how many days will 30 men do the same work?
Answer
Men: Days:: Men : Days
72 : 25 :: 30 : x
∴ By inverse proportion
72 × 25 = 30 × x
⇒ x = (25×72)/30
= 60 days
Question 7 :-
If 56 workers can build a wall in 180 hours, how many workers will be required to do the same work in 70 hours?
Answer
Workers: Hours:: Workers: Hours
56 : 180 :: x : 70
∴ By inverse proportion
56 × 180 = x × 70
⇒ x = (180×56)/70
= 144 workers
Question 8 :-
A car takes 6 hours to reach a destination by travelling at the speed of 50 km per hour. How long will it take when the car travels at the speed of 75 km per hour?
Answer:
Time: Distance:: Time: Distance
6 : 50 km :: x : 75
∴ By inverse proportion
6 × 50 = x × 75
⇒ x = (50×6)/75
= 4 hours
Direct and Inverse Variations Exe-10 C for ICSE Class-8th
Question 1 :-
Cost of 24 identical articles is Rs. 108, Find the cost of 40 similar articles.
Answer
Cost of 24 identical articles = Rs.108
∴ Cost of 1 identical articles = Rs. 108/24
∴ Cost of 40 identical articles = Rs. ((108/24)×40)
= Rs. (108/3)×5
= Rs. 36 × 5
= Rs.180
Question 2 :-
If 15 men can complete a piece of work in 30 days, in how many days will 18 men complete it?
Answer:
Since 15 men can complete a piece of work in = 30 days
∴ 1 man can do the work in = 30 × 15 days
∴ 18 men can do the work in =(30×15)/18 = (5×15)/3
= 5 × 5 = 25 days
Hence 18 men can do the work in 25 days.
Question 3 :-
In order to complete a work in 28 days, 60 men are required. How many men will be required if the same work is to be completed in 40 days?
Answer:
Let x be number of men required 60 men can do the work in = 28 days
1 man can do the work in = 28 x 60 days
x man can do the work in = (28×60)/x day
But (28×60)/x = 40 days ……(Given)
∴ x = (28×60)/40 =7 × 6 = 42
Required number of men = 42
Question 4 :-
A fort had provisions for 450 soldiers for 40 days. After 10 days, 90 more soldiers come to the fort. Find in how many days will the remaining provisions last at the same rate?
Answer:
After 10 days :
For 450 soldiers, provision is sufficient for (40 – 10) days = 30 days
For 1 soldier, provision is sufficient for 30 × 450 days
For 540 soldiers, the provision is sufficient for
= (30×450)/540 = (30×50)/60 = 50/2 = 25 days
Question 5 :-
A garrison has sufficient provisions for 480 men for 12 days. If the number of men is reduced by 160; find how long will the provisions last.
Answer:
Strength of garrison = 480 men
Strength reduced by = 160 men
New strength of garrison = 480 − 160 = 320
Provision for 480 men lasts for = 12 days
Provision for 1 man last for = 480 × 12 days
Provision for 320 men lasts for = (480×12)/320 days
= (3×12)/2 = 18 days
Question 6 :-
3/5 quintal of wheat costs Rs.210. Find the cost of :
(i) 1 quintal of wheat
(ii) 0.4 quintal of wheat
Answer:
(i) 3/5 quintal of wheat costs = Rs.210
1 quintal of wheat costs = 210×(3/5) = 70 x 5 = Rs.350
(ii) 1 quintal of wheat costs = Rs.350
0.4 quintal of wheat costs = 350 x 0.4 = Rs. 140.0 = Rs.140
Question 7 :-
If 2/9 of a property costs Rs.2,52,000; find the cost of 4/7 of it.
Answer:
2/9 of property costs = Rs.252000
1 of a property costs = Rs. 252000×(9/2)
= Rs. 2268000/2
= Rs.1134000
4/7 of a property costs = 1134000×(4/7)
= 162000 × 4
= Rs.6,48,000
Question 8 :-
4 men or 6 women earn Rs. 360 in one day. Find, how much will:
(i) a man earn in one day?
(ii) a woman earn in one day?
(iii) 6 men and 4 women earn in one day?
Answer:
4 men earn Rs. 360 in one day
(i) 1 man can earn = Rs.360/4 = Rs.90 in one day
(ii) 6 women earn Rs. 360 in one day
1 woman can earn Rs.360/6 = Rs.60 in one day
(iii) ∴ 6 men and 4 women earn in one day
= 6 × 90 + 4 × 60 = 540 + 240 = Rs.780
Question 9 :-
16 boys went to the canteen to have tea and snacks together. The bill amounted to Rs. 114.40. What will be the contribution of a boy who pays for himself and 5 others?
Answer:
16 boys pay for bill = Rs.114.40
1 boy pays for bill = Rs.114.40/16 = Rs. 7.15
∴ Contribution of a boy who pays for himself and 5 others = 6 × 7.15 = Rs.42.90
Question 10 :-
50 labourers can dig a pond in 16 days. How many labourers will be required to dig another pond, double in size in 20 days?
Answer:
In 16 days for diging pond labour reqd.
In 1 day, labour reqd. = 50 × 16
In 20 days, labour reqd. = (50×16)/20
In 20 days, with double work, labour reqd.
= (50×16×2)/20
= 5 × 8 × 2
= 80
Hence labourers required = 80
Question 11 :-
If 12 men or 18 women can complete a piece of work in 7 days, in how many days can 4 men and 8 women complete the same work?
Answer:
12 men = 18 women
∴ 4 m = (18/12)×4
= 6 women
Total women in second case = 4 men + 8 women
6 + 8 = 14 women
18 women can do a piece of work in 7 days
Let 14 women will do the same work in x days
∴ 18: 14: : 7: x ……..(Less women, more days)
⇒ 18 : 14 : : x : 7
x = (18×7)/14 .……(Using inverse proportion)
= 9
∴ They will complete the work in 9 days
Question 12 :-
If 3 men or 6 boys can finish a work in 20 days, how long will 4 men and 12 boys take to finish the same work ?
Answer:
3 men = 6 boys
4 men = (6/3)×4 = 8
Total boys in second case :
= 4 men + 12 boys = 8 + 12 = 20 boys
6 boys can do a piece of work in 20 days
Then let 20 boys will do the same work in x days
∴ 6 : 20 : : 20 : x ……..(More boys,less days)
⇒ 6 : 20 : : x : 20 ….(By inverse proportion)
x = (20×6)/20
= 6 days
∴ They will do the work in 6 days
Question 13 :-
A particular work can be completed by 6 men and 6 women in 24 days; whereas the same work can be completed by 8 men and 12 women in 15 days. Find :
(i) according to the amount of work done, one man is equivalent to how many women.
(ii) the time taken by 4 men and 6 women to complete the same work.
Answer:
6 men + 6 women can finish the work in = 24 days
144 men + 144 women can finish it in = 1 day
8 m + 12 women can finish the work in = 15 days
120 men + 180 women can finish it in = 1 day
(i) 144 men + 144 women = 120 men + 180 women
⇒ 144 men – 120 men
= 180 – women – 144 women
⇒ 24 men = 36 women
1 man =36/24
=3/2 women
=1 (1/2) women
(ii) Case first
6×(3/2) + 6 = 9+6
= 15 women
Case second
4×(3/2)+6
= 6 + 6
= 12 women
Now, 15 women can do a piece of work in = 24 days
1 women will do it in = 24 × 15 days
and 12 women will do it in
= (24×15)/12
= 30 days
Question 14 :-
If 12 men and 16 boys can do a piece of work in 5 days and, 13 men and 24 boys can do it in 4 days, how long will 7 men and 10 boys take to do it?
Answer:
12 men + 16 boys can do a piece of work in = 5 days
60 men + 80 boys can do a piece of work in = 1 day ………. (i)
and 13 men + 24 boys can do the same work in = 4 days
52 men + 96 boys can do the same work in = 1 day ………….(ii)
From (i) and (ii)
60 men + 80 boys = 52 men + 96 boys
⇒ 60 men – 52 men = 96 boys – 80 boys
⇒ 8 men = 16 boys
1 man =16/8 = boys
Now, case first ,
12 men + 16 boys = 12 x 2 + 16 = 24+16 = 40 boys
case second ,
7 men + 10 boys = 7 x 2 + 10 = 14 + 10 = 24 boys
Now 40 boys can do a piece of work in = 5 days
1 boy can do the same work in = 5 x 40 days
and 24 boys will do the same work in
= (5 × 40)/24 days
= 25/3
= 8(1/3) days
Direct and Inverse Variations ICSE Class-8th Exe-10 D
Question 1 :-
Eight oranges can be bought for Rs. 10.40. How many more can be bought for Rs. 16.90?
Answer:
Number of oranges bought for Rs. 10.40 = 8
Number of oranges bought for Rs.1 =8/10.40
Number of oranges bought for Rs.16.90
= (8/10.40)×16.90 = (8×1690)/1040 = 13520/1040 = 13
∴ Number of more oranges which can be bought for Rs.16.90 = 13 − 8 = 5
Question 2 :-
Fifteen men can build a wall in 60 days. How many more men are required to build another wall of same size in 45 days?
Answer:
In 60 days a wall can be built by = 15 men
In 1 day a wall can be built by = 15 x 60 men
In 45 days a wall can be built by = (15×60)/45 = 900/45 = 20 men
No. of more men required to build the wall in 45 days = 20 – 15 = 5 men
Question 3 :-
Six taps can fill an empty cistern in 8 hours. How much more time will be taken, if two taps go out of order? Assume, all the taps supply water at the same rate.
Answer:
Total no. of taps = 6
Out of order taps = 2
Taps in working condition = 6 – 2 = 4
6 taps can fill an empty cistern in = 8 hours
1 tap can fill an empty cistern in = 6 x 8 hours
4 taps can fill an empty cistern in = 48/4 = 12 hours
More time taken when 2 taps are out of order = 12 – 8 = 4 hour
Question 4 :-
A contractor undertakes to dig a canal, 6 kilometres long, in 35 days and employed 90 men. He finds that after 20 days only 2 km of canal have been completed. How many more men must be employed to finish the work in time?
Answer:
Length of canal = 6 km
In 20 days canal made = 2 km
Remaining length of canal = 6 – 2 = 4 km
Remaining time = 35 – 20 = 15 days
In 20 days 2 km canal is made by = 90 men
In 1 day 2 km canal is made by = 90 x 20 men
In 15 days 2 km canal is made by = (90×20)/15 men
In 15 days 1 km canal is made by = (90×20)/(15×2) men
In 15 days 4 km canal is made by = (90×20×4)/(15×2) men = 6 x 10 x 4 men = 240 men
Number of more men to be employed to finish the work in time = 240-90 = 150 men
Question 5 :-
If 10 horses consume 18 bushels in 36 days. How long will 24 bushels last for 30 horses?
Answer:
10 horses consume 18 bushels in = 36 days
1 horse consumes 18 bushels in = 36 × 10 days = 360 days
30 horses consume 18 bushels in =360/30 days
= 12 days
30 horse consume 1 bushel in =1218 days
30 horse consume 24 bushels in
= (12/18)×24 days
= (2/3)×24 days
= 16 days
Question 6 :-
A family of 5 persons can be maintained for 20 days with Rs.2,480. Find, how long Rs.6944 maintain a family of 8 persons
Answer:
A family of 5 persons can be maintained with Rs.2480 for = 20 days
A family of 5 persons can be maintained with Rs.1 for =202/480 days
A family of 5 persons can be maintained with
Rs. 6944 = (20/2480) × 6944 = (1/124)×6944
= 56 days
A family of 1 person can be maintained
= 56 × 5 days
A family of 8 persons can be maintained
= (56×5)/8 days
= 7 × 5 days
= 35 days
Question 7 :-
90 men can complete a work in 24 days working 8 hours a day. How many men are required to complete the same work in 18 days working 7 hours a day?
Answer:
In 24 days, working 8 hours a day, work can be completed by = 90 men
In 1 day, working 8 hours a day, work can be completed by = 90 × 24 men
In 18 days, working 8 hours a day, work can be completed by = (90×24)/18 men
In 18 days, working 1 hour a day, work can be completed by = (90×24×8)/18 men
In 18 days, working 7 (1/2) i.e. 15/2 hours a day, work can be completed by
= (90×24×8)/18 × (2/15) men
= (90×24×8×2)/ (18×15) = (1×24×8×2)/3 = 128 men
Question 8 :-
Twelve typists, all working with same speed, type a certain number of pages in 18 days working 8 hours a day. Find, how many hours per day must sixteen typists work in order to type the same number of pages in 9 days?
Answer:
12 typists can type in 18 days with the number of working hours in day = 8 hours
1 typist can type in 18 days = 8 x 12 hour
1 typist can type in 9 days = 2 (8 x 12) hour
16 typist can type in a day = 2(8×12)/16 = 12 hours
Question 9 :-
If 25 horses consume 18 quintal in 36 days, how long will 28 quintal last for 30 horses?
Answer:
25 horses consume 18 quintal in = 36 days
1 horse consume 1 quintal in = (36×25)/(18×30) days
30 horses consume 28 quintal in = (36×25×28)/(18×30)days
= (2×5×28)/6 = 140/3 = 46(2/3) days
Question 10 :-
If 70 men dig 15,000 sq. m of a field in 5 days, how many men will dig 22,500 sq. m field in 25 days?
Answer:
70 men dig 15,000 sq. m of a field in 5 days
1 man can dig 15,000 sq. m of a field in = (5×70)/15,000
Men required to dig 22,500 sq. m. a field in 25 days

Hence required to dig 22,500 sq. m field in 25 days = 21
Question 11 :-
A contractor undertakes to build a wall 1000 m long in 50 days. He employs 56 men, but at the end of 27 days, he finds that only 448 m of wall is built. How many extra men must the contractor employ so that the wall is completed in time ?
Answer:
Number of men employed in the beginning = 56
Length of wall = 1000 m No. of days = 50
In the time of 27 days, only 448 m of the wall was completed
Remaining period = 50 – 27 = 23 days
and length of wall to be completed = 1000 – 448 = 552
Now in 27 days, 448 m long wall was completed by = 1000 m
in 1 day, 448 m long was completed by = 56 x 27
in 1 day, 1 m long wall will be completed by
= (56×27)/448 m
and in 23 days 552 m long wall be completed by
= (56×27×552)/(448×25) men
= (1×27×24)/8 = 81 men
∴ No. of extra men required
= 81 − 56 = 25 men
Question 12 :-
A group of labourers promises to do a piece of work in 10 days, but five of them become absent. If the remaining labourers complete the work in 12 days, find their original number in the group.
Answer:
Total period = 10 days
But work completed in = 12 days
No. of men was absent = 5
Let the number of men in the beginning = x
Now x men can do piece work in = 10 days
1 man will do it in = 10x × days
and (x − 5) will do it in =(10×X)/(x-5) days
∴ 10x/(x-5) =12
⇒ 10x = 12x − 60
⇒ 12x − 10x = 60 ⇒ 2x = 60
⇒ x = 60/2 = 30
∴ No. of men in the beginning = 30
Question 13 :-
Ten men, working for 6 days of 10 hours each, finish of a piece of work. How many men working at the same rate and for the same number of hours each day, will be required to complete the remaining work in 8 days?
Answer:
Work does one = 5/21
Remaining work = 1- (5/21) = (16/21)
5/21 of a work can be done in 6 days working 10 hours a day by = 10 m
1 work can be done in 6 days working 10 hours a day by = (10×21)/5
1 work can be done in 1 day working 10 hours a day by = (10×21×6)/5 men
16/21 work can be done in 8 days working 10 hours a day by
= (10×21×6×16)/(5×21×8) = 24 men
ICSE Class-8th Concise Selina Mathematics Exercise – 10 E
Question 1 :-
A can do a piece of work in 10 days and B in 15 days. How long will they take together to finish it ?
Answer:
A’s 1-day work = 1/10
B’s 1-day work = 1/15
(A + B)’s 1-day work = (1/10)+(1/15)
= (3+2)/30 = 5/30
= 1/6
∴ Both A and B together can finish the work in = 6 days
Question 2 :-
A and B together can do a piece of work in 6 days ; but B alone can do it in 10 days. How long will A take to do it alone?
Answer:
A and B can do the work in =6(2/3)days = (20/3) days
B can do the work in = 10 days
∴ (A + B)’s 1-day work = (3/20)
B’s 1-day work =1/10
A’s 1-day work =(3/20)-(1/10)
= (3-2)/20 = 120
∴ A can do the work in = 20
Question 3 :-
A can do a work in 15 days and B in 20 days. If they together work on it for 4 days ; what fraction of the work will be left ?
Answer:
A’s 1-day work = 1/15
B’s 1-day work = 1/20
(A+B)’s 1-day work =(1/15) + (1/20)
= (4+3)/60 = 7/60
(A+B)’s 4 days work =(7/60)×4=71/5
Remaining work = 1-(7/15) = (15-7)/15
=8/15
Question 4 :-
A, B and C can do a piece of work in 6 days, 12 days and 24 days respectively. In what time will they all together do it?
Answer:
A can do a piece of work in = 6 days
B can do a piece of work in = 12 days
C can do a piece of work in = 24 days
∴ A’s 1-day work =1/6
∴ B’s 1-day work = 1/12
∴ C’s 1-day work = 1/24
(A+B+C)’s 1-day work = (1/6) + (1/12) + (1/24)
= (4+2+1)/24 = 7/24
∴ (A+B+C) can do the work in = 24/7 days
= 3 (3/7) days
Question 5 :-
A and B working together can mow a field in 56 days and with the help of C, they could have mowed it in 42 days. How long would C take by himself?
Answer:-
(A+B) can mow a field in = 56 days
(A+B+C) can mow a field in = 42 days
∴ (A+B)’s 1 day work =1/56
(A+B+C)’s 1 day work =1/42
C’s 1 day work = (1/42)-(1/56)
= (4-3)/168
= 1/168
L.C.M. = 2 × 7 × 3 × 4 = 168
∴ C can do the work in = 168 days
Question 6 :-
A can do a piece of work in 24 days, A and B can do it in 16 days and A, B and C in 10 days. In how many days can A and C do it?
Answer:
A can do a piece of work in = 24 days
(A+B) can do a piece of work in = 16 days
(A+B+C) can do a piece of work in
= 10(2/3) days = 32/3 days
∴ A’s 1-day work =1/24
(A+B)’s 1 day work =1/16
(A+B+C)’s 1 day work =3/32
C’s 1 day work =(3/32)-(1/16)
= (3-2)/32=1/32
(A+C)’s 1-day work = (1/24) + (1/32)
= (4+3)/96 = 7/96
∴ (A+C) can do the work in =96/7 days
=13 (5/7) days
Question 7 :-
A can do a piece of work in 20 days and B in 15 days. They worked together on it for 6 days and then A left. How long will B take to finish the remaining work?
Answer:
Given,
A can do a piece of work in = 20 days
B can do a piece of work in = 15 days
∴ A’s 1-day work =1/20
B’s 1-day work = 1/15
(A+B)’s 1-day work =(1/20)+(1/15)
=(3+4)/60=7/60
(A+B)’s 6 days work = (7/60)×6 = 7/10
Remaining work = 1 – (7/10)
= (10-7)/10 = 3/10
B can do 1 work in = 15 days
B can do 3/10 work in = 15×(3/10) days
=45/10 days = 9/2 days = 4(1/2) days
Question 8 :-
A can finish a piece of work in 15 days and B can do it in 10 days. They worked together for 2 days and then B goes away. In how many days will A finish the remaining work?
Answer:
A can finish a piece of work in = 15 days
B can finish a piece of work in = 10 days
∴ A’s 1 day work = 1/15
B’s 1-day work = 1/10
(A+B)’s 1-day work = (1/15)+(1/10)
= (2+3)/30 = 5/30=1/6
(A+B)’s 2 days work = 1/6 × 2 = 1/3
Remaining work which will be done by A alone
= 1- (1/3) = (3-1)/3=2/3
∴ A can finish 1 work in = 15 days
A can finish 2/3 work in = 15×(2/3) days
=30/3 days = 10 days
Question 9 :-
A can do a piece of work in 10 days ; B in 18 days; and A, B and C together in 4 days. In what time would C alone do it ?
Answer:
A can do a piece of work in = 10 days
B can do a piece of work in = 18 days
(A+B+C) can do a piece of work in = 4 days
∴ A’s 1-day work =1/10
B’s 1-day work = 1/18
(A+B)’s 1-day work = (1/10) + (1/18) = (9+5)/90
= 14/90 = 7/45
(A+B+C)’s 1-day work =1/4
∴ C’s 1-day work =(1/4)-(7/45)
= (45-28)/180= 17/180
∴ C can do the piece of work in = 180/17 days
=10 (10/17) days
Question 10 :-
A can do of a work in 5 days and B can do
of the same work in 10 days. Find the number of days in which both working together will complete the work.
Answer:
A can-do 1/4 of work in = 5 days
A can-do 1 work in = 5 × 4 days
= 20 days
B can do 1/3 of work in = 10 days
B can do 1 work in = 10 × 3 days
= 30 days
A’s 1-day work =1/20
B’s 1-day work =1/30
(A+B)’s 1 day work =(1/20)+(1/30)
=(3+2)/60
= 5/60
= 1/12
∴ A and B working together will complete the work in = 12 days
Question 11 :-
One tap can fill a cistern in 3 hours and the waste pipe can empty the full cistern in 5 hours. In what time will the empty cistern be full, if the tap and the waste pipe are kept open together?
Answer:
One tap can fill a cistern in = 3 hours
A waste pipe can empty a cistern in = 5 hours
∴ One trap 1-hour work =1/3
Waste pipe 1-hour work =1/5
∴ One tap and waste pipe together 1-hour work
= (1/3)-(1/5)=(5-3)/15
= 2/15
∴ The empty cistern will be full in =15/2 hours
=7(1/2) hours
Question 12 :-
A and B can do a work in 8 days; B and C in 12 days, and A and C in 16 days. In what time could they do it, all working together?
Answer:
A and B can do a work in = 8 days
B and C can do a work in = 12 days
A and C can do a work in = 16 days
(A+B)’s 1-day work =1/8
(B+C)’s 1-day work =1/12
(A+C)’s 1-day work =1/16
∴ [(A+B)+(B+C)+(A+C)]’s 1 day work
=18+112+116
i.e. [A+B+B+C+A+C]’s 1 day work
= (1/8) + (1/12) + (1/16)
= (6+4+3)/48 = 13/48
i.e. 2(A+B+C)’s 1-day work =13/48
i.e. (A+B+C)’s 1-day work =(13/48)×)1/2)=13/96
∴ (A+B+C) can do the work in =96/13days
=7(5/13) days
Question 13 :-
A and B complete a piece of work in 24 days. B and C do the same work in 36 days ; and A, B and C together finish it in 18 days. In how many days will (i) A alone,
(ii) C alone,
(iii) A and C together, complete the work?
Answer:
A and B complete a piece of work in = 24 days
B and C complete a piece of work in = 36 days
(A+B+C) complete a piece of work in = 18 days
(A+B)’s 1-day work = 1/24
(B+C)’s 1-day work = 1/36
(A+B+C)’s 1-day work = 1/18
(i) A’s 1-day work =(1/18)-(1/36)
= (2-1)/36=1/36
∴ A will complete the work in = 36 days
(ii) C’s 1-day work =(1/18)-(1/24)
=(4-3)/72=1/72
∴ C will complete the work in = 72 days
(iii) (A+C)’s 1-day work =(1/36)+(1/72)
= )2+1)/72=3/72
=1/24
∴ (A+C) will complete the work in = 24 days
Question 14 :-
A and B can do a piece of work in 40 days; B and C in 30 days; and C and A in 24 days.
(i) How long will it take them to do the work together?
(ii) In what time can each finish it working alone?
Answer:
A and B can do a piece of work in = 40 days
B and C can do a piece of work in = 30 days
C and A can do a piece of work in = 24 days
(A+B)’s 1-day work =1/40
(B+C)’s 1-day work =1/30
(C+A)’s 1-day work =1/24
(i) [(A+B)+(B+C)+(C+A)]’s 1 day work = (1/4)+(1/30)+(1/24)
= (3+4+5)/120
= 12/120 = 1/10
i.e. (A+B+B+C+C+A)’s 1-day work =1/10
i.e. 2 (A+B+C)’s 1-day work =1/10
∴ (A+B+C)’s 1-day work =(1/10)×(1/2)
=1/20
∴ (A+B+C) can do the work in = 20 days
(ii) A’s 1-day work =(1/20)-(1/30)
=(3-2)/60=1/60
∴ A can do the work in 60 days
B’s 1-day work =1/20-1/24
= (6-5)/120=1/120
∴ B can do the work in 120 days
now, C’s 1-day work =(1/20)-(1/40)
= (2-1)/40 = 1/40
C can do the work in 40 days
Hence A can do the work in = 60 days
B can do the work in = 120 days
C can do the work in = 40 days
Question 15 :-
A can do a piece of work in 10 days, B in 12 days and C in 15 days. All begin together but A leaves the work after 2 days and B leaves 3 days before the work is finished. How long did the work last?
Answer :-
A’s one day’s work =1/10
B’s one day’s work =1/12
C’s one day’s work =1/15
A, B and C’s one day’s work =(1/10)+(1/12)+(1/15)
= (6+5+4)/60 = 15/60 = 1/4
Let the work completed in x days
∴ A’s 2 days work + B’s (x − 3) days work + C’s x days work = 1

⇒ 9x = 60 − 12 + 15
⇒ 9x = 63
⇒ x = 63/9 = 7
∴ Work will last for 7 days
Question 16 :-
Two pipes P and Q would fill an empty cistern in 24 minutes and 32 minutes respectively. Both the pipes being opened together, find when the first pipe must be turned off so that the empty cistern may be just filled in 16 minutes.
Answer :-
P’s one minute’s work =1/24
Q’s one minute’s work =1/32
Let the first pipe must turn off x minutes
The cistern filled in 16 minutes
Then P’s x minutes work + Q’s 16 minutes work = 1

∴ After 12 minute pipe P would turned off
— End of Direct and Inverse Variations Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -8
Thanks