ML Aggarwal Circles Exe-15.3 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-15.3 Questions for Circles as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Circles Exe-15.3 Class 10 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 10th |
| Chapter-15 | Circles |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-15.3 Questions |
| Edition | 2022-2023 |
Circles Exe-15.3
ML Aggarwal Class 10 ICSE Maths Solutions
(Page 361)
Question 1. Find the length of the tangent drawn to a circle of radius 3 cm, from a point distant 5 cm from the centre.
Answer :
In a circle with centre O and radius 3 cm and P is at a distance of 5 cm.
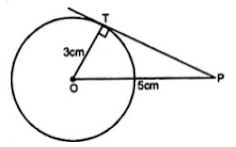
OT = 3 cm, OP = 5 cm
OT is the radius of the circle
OT ⊥ PT
Now, in right ∆ OTP.
By Pythagoras axiom,
OP2 = OT2 + PT2
⇒ (5)2 = (3)2 + PT2
⇒ PT2 = (5)2 – (3)2 = 25 – 9 = 16 = (4)2
⇒ PT = 4 cm.
Question 2. A point P is at a distance 13 cm from the centre C of a circle and PT is a tangent to the given circle. If PT = 12 cm, find the radius of the circle.
Answer :
CT is the radius
CP = 13 cm and tangent PT = 12 cm
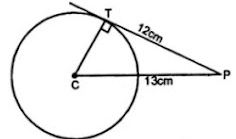
CT is the radius and TP is the tangent
CT is perpendicular TP
Now in right angled triangle CPT,
CP2 = CT2 + PT2 [using Pythagoras axiom]
⇒ (13)2 = (CT)2 + (12)2
⇒ 169 = (CT)2 + 144
⇒ (CT)2 = 169 -144 =25 = (5)2
⇒ CT = 5 cm.
Hence,
the radius of the circle is 5 cm.
Question 3. The tangent to a circle of radius 6 cm from an external point P, is of length 8 cm. Calculate the distance of P from the nearest point of the circle.
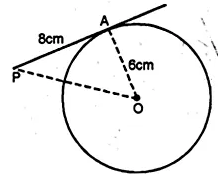
Answer :
Radius of the circle = 6 cm
and length of tangent = 8 cm
Let OP be the distance
i.e. OA = 6 cm, AP = 8 cm,
OA is the radius
OA ⊥ AP
Now In right ∆OAP,
OP2 = OA2 + AP2 (By Pythagoras axiom)
= (6)2 + (8)2
= 36 + 64
= 100
= (10)2
⇒ OP = 10 cm
Question 4. Two concentric circles are of the radii 13 cm and 5 cm. Find the length of the chord of the outer circle which touches the inner circle.
Answer :
Two concentric circles with centre O
OP and OB are the radii of the circles respectively, then
OP = 5 cm, OB = 13 cm.
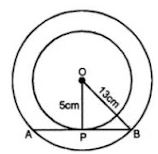
AB is the chord of outer circle which touches the inner circle at P.
OP is the radius and APB is the tangent to the inner circle.
In the right angled triangle OPB, by Pythagoras axiom,
OB2 = OP2 + PB2
⇒ 132 = 52 + PB2
⇒ 169 = 25 + PB2
⇒ PB2 = 169 – 25 = 144
⇒ PB = 12 cm
But P is the mid-point of AB.
AB = 2PB = 24 cm
Question 5. Two circles of radii 5 cm and 2.8 cm touch each other. Find the distance between their centers if they touch :
(i) externally
(ii) internally.
Answer :
Radii of the circles are 5 cm and 2.8 cm.
i.e. OP = 5 cm and CP = 2.8 cm.
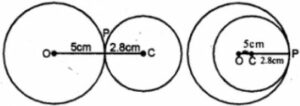
(i) When the circles touch externally,
then the distance between their centers = OC = 5 + 2.8 = 7.8 cm.
(ii) When the circles touch internally,
then the distance between their centers = OC = 5.0 – 2.8 = 2.2 cm
Question 6.
(a) In figure (i) given below, triangle ABC is circumscribed, find x.
(b) In figure (ii) given below, quadrilateral ABCD is circumscribed, find x.
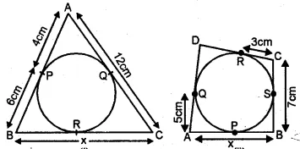
Answer :
(a) From A, AP and AQ are the tangents to the circle
∴ AQ = AP = 4cm
CQ = 12 – 4 = 8 cm.
From B, BP and BR are the tangents to the circle
BR = BP = 6 cm.
Similarly, from C,
CQ and CR the tangents
CR = CQ = 8 cm
⇒ x = BC = BR + CR = 6 cm + 8 cm = 14 cm
(b) From C, CR and CS are the tangents to the circle.
CS = CR = 3 cm.
But, BC = 7 cm.
⇒ BS = BC – CS = 7 – 3 =4 cm.
Now from B,BP and BS are the tangents to the circle.
BP = BS = 4 cm
From A, AP and AQ are the tangents to the circle.
AP = AQ = 5cm
⇒ x = AB = AP + BP = 5 + 4 = 9 cm
Question 7.
(a) In figure (i) given below, quadrilateral ABCD is circumscribed; find the perimeter of quadrilateral ABCD.
(b) In figure (ii) given below, quadrilateral ABCD is circumscribed and AD ⊥ DC ; find x if radius of incircle is 10 cm.
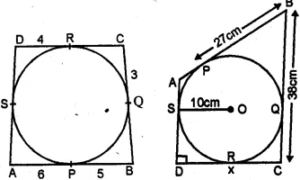
Answer :
(a) From A, AP and AS are the tangents to the circle
∴ AS = AP = 6
From B, BP and BQ are the tangents
∴ BQ = BP = 5
From C, CQ and CR are the tangents
CR = CQ
From D, DS and DR are the tangents
DS = DR = 4
Therefore, perimeter of the quadrilateral ABCD
= 6 + 5 + 5 + 3 + 3 + 4 + 4 + 6
= 36 cm
(b) in the circle with center O, radius OS = 10 cm
PB = 27 cm, BC = 38 cm
OS id the radius and AD is the tangent.
Therefore, OS perpendicular to AD.
SD = OS = 10 cm.
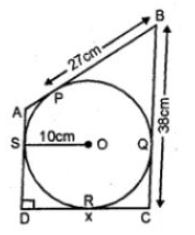
To the circle
DR = DS = 10 cm
From B, BP and BQ are tangents to the circle.
BQ = BP = 27 cm.
⇒ CQ = CB – BQ = 38 – 27 = 11 cm.
Now from C, CQ and CR are the tangents to the circle
CR = CQ = 11 cm.
⇒ DC = x = DR + CR = 10 + 11 = 21 cm
Circles Exe-15.3
ML Aggarwal Class 10 ICSE Maths Solutions
(Page 362)
Question 8
(a) In the figure (i) given below, O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, find the radius of the circle.
(b) In the figure (ii) given below, from an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D. If AP = 15 cm, find the perimeter of the triangle PEC.
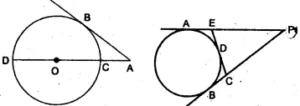
Answer :
(i) Join OB
∠OBA = 90°
(Radius through the point of contact is perpendicular to the tangent)
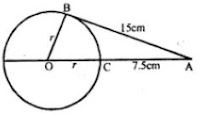
OB2 = OA2 – AB2
⇒ r2 = (r + 7.5)2 – 152
⇒ r2 = r2 + 56.25 + 15r – 225
⇒ 15r = 168.75
⇒ r = 11.25
Hence, radius of the circles = 11.25 cm
(ii) In the figure, PA and PB are the tangents
Drawn from P to the circle.
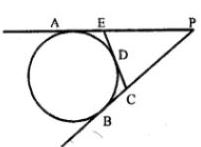
AP = 15 cm
PA and PB are tangents to the circle
AP = BP = 15 cm
Similarly EA and ED are tangents
EA = ED
Similarly BC = CD
Now perimeter of triangle PEC,
= PE + EC + PC
= PE + ED + CD + PC
= PE + EA + CB + PC (ED = EA and CB = CD)
= AP + PB
= 15 + 15
= 30 cm.
Question 9.
(a) If a, b, c are the sides of a right triangle where c is the hypotenuse, prove that the radius r of the circle which touches the sides of the triangle is given by
r=(a+b-c)/2
(b) In the given figure, PB is a tangent to a circle with centre O at B. AB is a chord of length 24 cm at a distance of 5 cm from the centre. If the length of the tangent is 20 cm, find the length of OP.
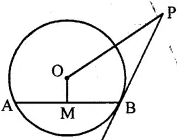
Answer :
(a) Let the circle touch the sides BC, CA and AB of the right triangle ABC at points D, E and F respectively,
where BC = a, CA = b
and AB = c (as showing in the given figure).
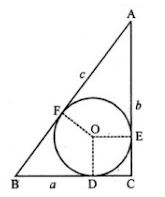
As the lengths of tangents drawn from an external point to a circle are equal
AE = AF, BD = BF and CD = DE
OD ⊥ BC and OE ⊥ CA (tangents is ⊥ to radius)
ODCE is a square of side r
DC = CE = r
AF = AE = AC – EC = b – r and,
BF = BD = BC – DC = a – r
Now,
AB = AF + BF
c = (b – r) + (a – r)
⇒ 2r = a + b – c
⇒ r = (a+b–c)/2
⇒ OP2 = 400 + 169
⇒ OP = a − √569cm

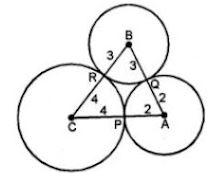
Question 10. Three circles of radii 2 cm, 3 cm and 4 cm touch each other externally. Find the perimeter of the triangle obtained on joining the centers of these circles.
Answer :
Three circles with centers A, B and C touch each other externally
at P, Q and R respectively and the radii of these circles are
2 cm, 3 cm and 4 cm.
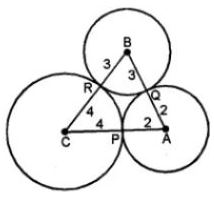
By joining the centers of triangle ABC formed in which,
AB = 2 + 3 = 5 cm
BC = 3 + 4 = 7 cm
CA = 4 + 2 = 6 cm
Therefore, perimeter of the triangle ABC = AB + BC + CA
= 5 + 7 + 6
= 18 cm
Question 11
(a) In the figure (i) given below, the sides of the quadrilateral touch the circle. Prove that AB + CD = BC + DA.
(b) In the figure (ii) given below, ABC is triangle with AB = 10cm, BC = 8cm and AC = 6cm (not drawn to scale). Three circles are drawn touching each other with vertices A, B and C as their centers. Find the radii of the three circles.
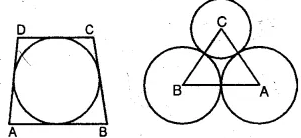
Answer :
(a) Given: Sides of quadrilateral ABCD touch the circle at
P, Q, R and S respectively.
To prove: AB + CD = BC + DA
Proof:
Tangents from A, AP and AS are to the circle.
∴ AP = AS
Similarly,
PB = BQ, CR = CQ and DR = DS
Adding them, we get
AP + PB + CR + DR = AS + BQ + CQ + DS
⇒ AP + PB + CR + DR = BQ + CQ + AS + SD
⇒ AB + CD = BC + DA
(b) AB = 10 cm, BC = 8 cm, AC = 6 cm
BP + PA = 10 cm …(i)
BC = 8 cm (given)
BR + RC = 8 cm
∴ BP + RC = 8 …(ii)
Again, AC = 6 cm
AQ + QC = 6 cm
PA + RC = 6 cm …(iii)
Adding, (i) + (ii) + (iii) we have
2 (BP + PA + RC) = 24 cm
∴ BP + PA + RC = 12 cm …(iv)
Now, (iv) – (i) we have
RC = 12 – 10 = 2 cm
Also, (iv) – (ii) we have
PA = 12 – 8 = 4 cm
Also, (iv) – (iii) we have
BP = 12 – 6 = 6 cm
Radii: BP = 6 cm, PA = 4 cm, RC = 2 cm
Circles Exe-15.3
ML Aggarwal Class 10 ICSE Maths Solutions
(Page 363)
Question 12 (Exe-15.3 Circles ML Aggarwal Solutions ICSE)
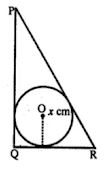
(a) ln the figure (i) PQ = 24 cm, QR = 7 cm and ∠PQR = 90°. Find the radius of the inscribed circle ∆PQR
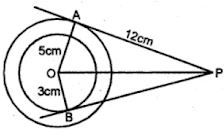
(b) In the figure (ii) given below, two concentric circles with centre O are of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
Answer :
(a) In the figure, a circle is inscribed in the triangle PQR
which touches the sides. O is centre of the circle.
PQ = 24cm, QR = 7 cm ∠PQR = 90°
OM is joined.
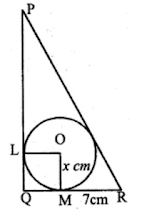
∵ OL and OM are the radii of the circle
∴ OL ⊥ PQ and OM ⊥ BC and ∠PQR = 90°
∴ QLOM is a square
∴ OL = OM = QL = QM.
Now in ΔPQR ∠O = 90°
∴ PQ2 = PQ2 + QR2
= (24)2 + (7)2
= 576 + 49
= 625
= (25)2
∴ P = 25 cm
Let OB = x, then
QM = QL = x
∵ PL and PN are the tangents to the circle.
PL = PN
⇒ PQ – LQ = PR – RN
⇒ 24 – x = 25 – PM (∵ RN = RM)
⇒ 24 – x = 25 – (QR – QM)
⇒ 24 – x = 25 – (7 – x)
⇒ 24 – x = 25 – 7 + x
⇒ 24 – 25 + 7 = 2x
⇒ 2x = 6
⇒ x = 6/2 = 3 cm
∴ Radius of the incircle = 3 cm
(b) Radius of outer circle = 5 cm
And radius of inner circle = 3 cm

∴ OA = 5 cm
OB = 3 cm and AP = 12 cm
∵ OA = 5 cm
OB = 3 cm and AP = 12 cm
∵ OA = 5 cm
OB = 3 cm and AP = 12 cm
∵ OA is radius and AP is the tangent.
∴ OA ⊥ AP
∴ In right ΔOAP
OP2 = OA2 + AP2
= (5)2 + (12)2
= 25 + 144
= 169
= (13)2
∴ OP = 13
Similarly in right ∠OBP
OP2 = OB2 + BP2
⇒ (13)2 = (3)2 + BP2
⇒ 169 = 9 + BP2
⇒ BP2 = 169 – 9 = 160
BP = √160
= √16 x 10
= 4 √10 cm
Question 13.
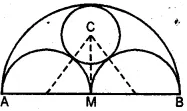
(a) In the figure (i) given below, AB = 8 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all three semi-circles as shown, find its radius.
Figure see in your text book
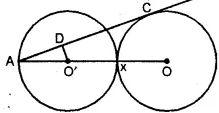
(b) In the figure (ii) given below, equal circles with centres O and O’ touch each other at X. OO’ is produced to meet a circle O’ at A. AC is tangent to the circle whose centre is O. O’D is perpendicular to AC. Find the value of :
(i) AO′/AO
(ii) area of ΔADO′/area of ΔACO
Answer :
(a) Let x be the radius of the circle with centre C and radii of each equal
CP = x + 2 and CM = 4 – x
∴ In right ΔPCM
(PC)2 = (PM)2 + (CM)2
⇒ (x + 2)2 = (2)2 + (4 – x)2
⇒ x2 + 4x + 4 = 4 + 16 – 8x + x2
⇒ 4x + 8x + 4 – 4 – 16 = 0
⇒ 12x = 16
⇒ x = 16/12 = 4/3 cm
∴ Radius = 4/3 cm.
(b) Two equal circles with centre O and O’ touch each other externally at X. OO’ is joined and produced to meet the circle at A. AC is the tangent to the circle with centre O. O’D is ⊥ AC. Join AC.
∵ OC is radius and AC is tangent, then OC ⊥ AC.
Let radius of each equal circle = r.
∠A = ∠A (Common)
∠D = ∠C (each 90°)
∴ ΔADO’ ~ ΔACO (AA axiom of similarity)
(i) ∴ AO’/AO = r/3r = 1/3
(ii) ∵ ΔADO’ ~ ΔACO
∴ (area of ΔADO’)/(area of ΔACO)
= (AO’)2/(AO)2
= (1/3)2 (from (i))
= 1/9
Circles Exe-15.3
ML Aggarwal Class 10 ICSE Maths Solutions
(Page 364)
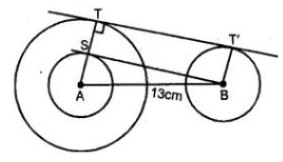
Question 14. The length of the direct common tangent to two circles of radii 12 cm and 4 cm is 15 cm. Calculate the distance between their centers.
Answer :
Let R and r be the radii of the circles
with centre A and B respectively
Let TT’ be their common tangent.
∴ (TT)2 = (AB)2 – (R – r)2
⇒ (15)2 = (AB)2 – (12 – 4)2
⇒ 225 = AB2 – (8)2
⇒ (AB)2 = 225 + 64
= 289
= (17)2
∴ AB = 17 cm
Hence distance between their centers = 17 cm Ans.
Question 15. Calculate the length of a direct common tangent to two circles of radii 3 cm and 8 cm with their centers 13 cm a part.
Answer :
Let A and B be the centers of the circles
whose radii are 8 cm and 3 cm and
let TT’ length of their common tangent and AB = 13 cm.
Now (TT’)2 = (AB)2 – (R – r)2
= (13) – (8 – 3)2
= 169 – (5)2
= 169 – 25
= 144
= (12)2
∴ TT’ = 12 cm
Hence, length of common tangent = 12 cm.
Question 16. In the given figure, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively. Given that AB = 8 cm, calculate PQ.
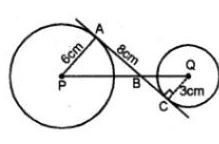
Answer :
AC is a transverse common tangent to the two circles
with centre P and Q and of radii 6 cm and 3 cm respectively
AB = 8 cm. Join AP and CQ.

In right ΔPAB,
PB2 = PA2 + AB2
= 62 + 82
= 36 + 64
= 100
= 102
∴ PB = 10 cm
Now in ΔPAB and ΔBCQ,
∴ ∠A = ∠C (each 90°)
∠ABP = ∠CBQ (vertically opposite angles)
∴ ΔPAB ~ ∠BCQ (AA axiom of similarity)
∴ AP/CQ = PB/BQ
⇒ 6/3 = 10/BQ
⇒ BQ = (10×3)/6 = 5 cm
∴ PQ = PB + BQ
= 10 + 5
= 15 cm.
Question 17. Two circles with centers A, B are of radii 6 cm and 3 cm respectively. If AB = 15 cm, find the length of a transverse common tangent to these circles.
Answer :
AB = 15 cm.
Radius of the circle with centre A = 6 cm
and radius of second circle with radius B = 3 cm.
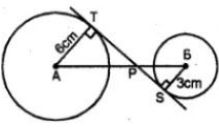
Let AP = x, then PB = 15 – x
In ΔATP and ΔSBP
∠T = ∠S (each 90°)
∠APT = ∠BPS (vertically opposite angles)
∴ ΔATP ~ ΔSBP (AA axiom of similarity)
AT/BS = AP/PB
⇒ 6/3 = x/(15–x)
⇒ x/(15–x) = 6/3
⇒ 3x = 90 – 6x
⇒ 3x + 6x = 90
⇒ 9x = 90
∴ x = 90/9 = 10
∴ AP = 10 cm,
PB = 15 – 10 = 5 cm
Now in right ΔATP,
AP2 = AT2 + TP2
⇒ (10)2 = (6)2 + TP2
⇒ 100 = 36 + TP2
⇒ TP2 = 100 – 36 = 64
⇒ TP2 = (8)2
∴ TP = 8 cm
Similarly in right ΔPSB,
PB2 = BS2 + PS2
⇒ (5)2 = (3)2 + PS2
⇒ 25 = 9 + PS2
⇒ PS2 = 25 – 9
= 16
= (4)2
∴ PS = 4 cm
Hence TS = TP + PS
= 8 + 4
= 12 cm
Question 18.
(a) In the figure (i) given below, PA and PB are tangents at a points A and B respectively of a circle with centre O. Q and R are points on the circle. If ∠APB = 70°, find (i) ∠AOB (ii) ∠AQB (iii) ∠ARB
(b) In the figure (ii) given below, two circles touch internally at P from an external point Q on the common tangent at P, two tangents QA and QB are drawn to the two circles. Prove that QA = QB.

Answer :
(a) To find : (i) ∠AOB, (ii) ∠AQB, (iii) ∠ARB
Given: PA and PB are tangents at the points A and B respectively
of a circle with centre O and OA and OB are radii on it.
∠APB = 70°
Construction: Join AB
∴ OAB = ∠OBA
(i) Since, AP and BP are tangents to the circle and OA and OB are radii on it.
∴ OA ⊥ OP and OB ⊥ BP
∴ ∠AQB = 180° – 70°
= 110°
(ii) Arc AB subtends ∠AOB at the centre and ∠AOB at the remaining part of the circle.
∴ ∠AQB = 2∠AOB
⇒ ∠AQB = ½ ∠AOB
⇒ ∠AQB = 1/2∠AOB
⇒ ∠AQB = ½ × 110° = 55°
(iii) Now in ΔOAB,
OA = OB
∴ ∠OAB = ∠OBA (Radii of the same circle)
= ½ (180° – 110°)
= ½ × 70°
= 35°
We know, ∠AOB = 110°
Reflex ∠AOB = 360° – 110°
= 250°
∴ ∠ARB = ½ of reflex ∠AOB (∵ Angle at the centre of a circle = double the angle at the remaining part of the circle)
= ½ × 250°
= 120°
(b) In the fig. (ii)
Two circles touch each other internally at P. From a point Q, outside, common tangents QP, QA and QB are drawn to the two circles.
To prove : QA = QB
Proof : From Q, QA and QP are the tangents to the outer circle.
∴ QP = QA …(i)
Similarly, from Q, QB and QP are the tangents to the inner circle.
∴ QP = QB …(ii)
From (i) and (ii)
QA = QB
Hence, proved.
Question 19. In the given figure, AD is a diameter of a circle with centre O and AB is tangent at A. C is a point on the circle such that DC produced intersects the tangent of B. If ∠ABC = 50°, find ∠AOC.
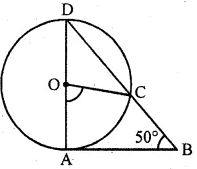
Answer :
Given AB is tangent to the circle at A and OA is radius, OA ⊥ AB
In ∆ABD
∠OAB + 90° + ∠ADC = 180°
⇒ ∠OAB + 90° + 50° = 180°
⇒ ∠OAB + 140° = 180°
⇒ ∠OAB + 180° – 140° = 40°
(∵ Angle at centre of a circle = double the angle at the remaining part of circle)
∴ ∠ABC = 2 × 40°
= 80°
Question 20
In the given figure, tangents PQ and PR are drawn from an external point P to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, Find ∠RQS
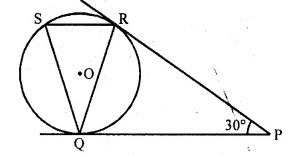
Answer :
In the given figure,
PQ and PR are tangents to the circle with centre O drawn from P
∠RPQ = 30°
Chord RS || PQ is drawn
To find ∠RQS
∴ PQ = PR (tangents to the circle)
∴ ∠PRQ = ∠PQR
But ∠RPO = 30°
∴ ∠PRO = ∠PQR = (180° – 30°)/2
= 150°/2
= 75°
And ∠RSQ = ∠QRS (∵ QR = QS)
= 75°
Now in ΔQRS,
∠RQS = 180° – (∠RSQ + ∠QRS)
= 180° – (75° + 75°)
= 180° – 150°
= 30°
Circles Exe-15.3
ML Aggarwal Class 10 ICSE Maths Solutions
(Page 365)
Question 21.
(a) In the figure (i) given below, PQ is a tangent to the circle at A, DB is a diameter, ∠ADB = 30° and ∠CBD = 60°, calculate (i) ∠QAB (ii) ∠PAD (iii) ∠CDB.

(b) In the figure (ii) given below, ABCD is a cyclic quadrilateral. The tangent to the circle at B meets DC produced at F. If ∠EAB = 85° and ∠BFC = 50°, find ∠CAB.
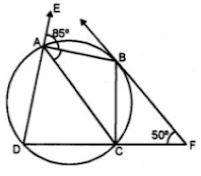
Answer :
(a) PQ is tangent and AD is chord
(i) ∴ ∠QAB = ∠BDA = 30°
(Angles in the alternate segment)
(ii) In ∆ADB,
∠DAB = 90° (Angle in a semi-circle)
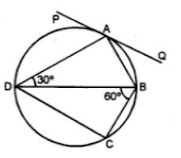
And ∠ADB = 30°
∴ ∠ABD = 180° – (90° + 30°)
= 180° – 120°
= 60°
But ∠PAD = ∠ABD (Angles in the alternate segment)
= 60°
(iii) In right ΔBCD
∠BCD = 90° (Angle is a semi-circle)
∠CBD = 60° (given)
∴ ∠CBD = 180° – (90° + 60°)
= 180° – 150°
= 30°
(b) ABCD is a cyclic quadrilateral.

∴ Ext. ∠EAB = ∠BCD
∴ ∠BCD = 85°
But ∠BCD + ∠BCF = 180° (Linear pair)
⇒ 85° + ∠BCF = 180°
∠BCF = 180° – 85° = 95°
Now in ΔBCF,
∠BCF + ∠BFC + ∠CBF = 180°
⇒ 95° + 50° + ∠CBF = 180°
⇒ 145° + ∠CBF = 180°
⇒ ∠CBF = 180° – 145° = 35°
∵ BF is a tangent and BC is the chord.
∴ ∠CAB = ∠CBF (Angles in the alternate segment)
⇒ ∠CAB = 35°
Question 22.
(a) In the figure (i) given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and z. (2015)
(b) In the figure (ii) given below, O is the centre of the circle. PS and PT are tangents and ∠SPT = 84°. Calculate the sizes of the angles TOS and TQS.
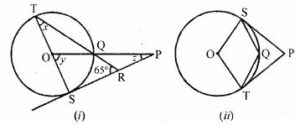
Answer :
Consider the following figure:
TS ⊥ SP,
∠TSR = ∠OSP = 90°
In ∆TSR,
∠TSR + ∠TRS + ∠RTS = 180°
⇒ 90° + 65° + x = 180°
⇒ x = 180° – 90° – 65°
⇒ x = 25°
⇒ y = 2x
[Angle subtended at the centre is double that of the angle subtended by the arc at the same centre]
⇒ y = 2 × 25°
⇒ y = 50°
In ΔOSP,
∠OSP + ∠SPO + ∠POS = 180°
⇒ 90° + z + 50° = 180°
⇒ z = 180° – 140°
∴ z = 40°
Hence x = 25°, y = 50° and z = 40°
(b) ∵ TP and SP are the tangents and OS and OT are the radii
∴ OS ⊥ SP and OT ⊥ SP
∴ ∠OSP = ∠OTP = 90°
∠SPT = 84°
But ∠SOT + ∠OTP + ∠TPS + OSP = 360°
⇒ ∠SOT + 90° + 84° + 90° = 360°
⇒ ∠SOT + 264° = 360°
⇒ ∠SOT = 360° – 26°
⇒ ∠SOT = 96°
And reflex ∠SOT = 360° – 96° = 264°
Now major arc ST subtends reflex ∠SOT at the centre and ∠TQS at the remaining part of the circle.
∴ ∠TQS = ½ reflex
∠SOT = ½ × 264° = 132°
Hence ∠TOS = 96° and ∠TQS = 132°
Question 23. In the adjoining figure, O is the centre of the circle. Tangents to the circle at A and B meet at C. If ∠ACO = 30°, find
(i) ∠BCO (ii) ∠AOR (iii) ∠APB
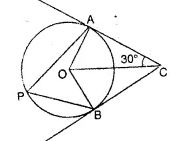
Answer :
(i) ∠BCO = ∠ACO = 30°
(∵ C is the intersecting point of tangent AC and BC)
(ii) ∠OAC = ∠OBC = 90°
∵ ∠AOC = ∠BOC = 180° – (90°+ 30°) = 60°
(∵ ∠AOB = ∠AOC + ∠BOC)
= 60° + 60°
= 120°
(iii) ∠APB = ½ ∠AOB
= 120°/2
= 60° [∵ angle subtended at the remaining part of the circle is half the subtended at the centre]
Question 24.
(a) In the figure (i) given below, O is the centre of the circle. The tangent at B and D meet at P. If AB is parallel to CD and ∠ ABC = 55°. find: (i)∠BOD (ii) ∠BPD
(b) In the figure (ii) given below. O is the centre of the circle. AB is a diameter, TPT’ is a tangent to the circle at P. If ∠BPT’ = 30°, calculate : (i)∠APT (ii) ∠BOP.
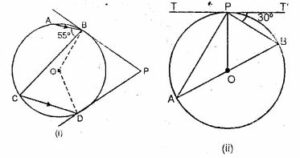
Answer :
(a) AB || CD
(i) ∠ABC = ∠BCD (Alternate angles)
⇒ ∠BCD = 55°
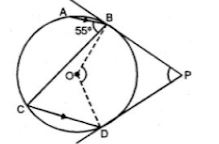
Now arc BD subtends ∠BOD at the centre and ∠BCD at the remaining part of the circle.
∴ ∠BOD = 2 ∠BCD
= 2 × 55°
= 110°
OB is radius and BP is tangent
∴ OB ⊥ BP°
Similarly, OD ⊥ DP
Now in quad. OBPD,
∠BOD + ∠ODP + ∠OBP + ∠BPD = 360° (Angles of quadrilateral)
⇒ 110° + 90° + 90° + ∠BPD = 360°
⇒ 290° + ∠BPD = 360°
⇒ ∠BPD = 360° – 290° = 70°
(b) TPT’ is the tangent.
(i) AB is diameter.
∴ ∠APB = 90° (Angle in a semi-circle)
And ∠BPT’ = 30°
∴ ∠APT = 180 ̊ – (90° + 30°)
= 180° – 120°
= 60°
(ii) TPT’ is tangent and PB is the chord.
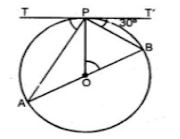
∴ ∠BAP = ∠BPT’ (Angles in the alternate segment)
= 30°
Now arc BP suntends ∠BOP at the centre and ∠BAP at the remaining part of the circle.
∠BOP = 2∠BAP
= 2×30°
= 60°
Circles Exe-15.3
ML Aggarwal Class 10 ICSE Maths Solutions
(Page 366)
Question 25. In the adjoining figure, ABCD is a cyclic quadrilateral.
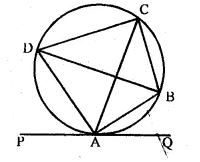
The line PQ is the tangent to the circle at A. If ∠CAQ : ∠CAP = 1 : 2, AB bisects ∠CAQ and AD bisects ∠CAP, then find the measure of the angles of the cyclic quadrilateral. Also prove that BD is a diameter of the circle.
Answer :
ABCD is a cyclic quadrilateral.
PAQ is the tangent to the circle at A.
∠CAD : ∠CAP = 1 : 2.
AB and AD are the bisectors of ∠CAQ and ∠CAP respectively
To prove:
(i) BD is the diameter of the circle.
(ii) Find the measure of the angles of the cyclic quadrilateral.
Proof:
(i) ∵ AB and AD are the bisectors of ∠CAQ and CAP respectively and
∠CAQ + ∠CAB = 180° (linear pair)
∴ ∠CAB = ∠CAD = 90°
⇒ ∠BAD = 90°
Hence, BD is at diameter of the circle.
(ii) ∴ ∠CAQ : ∠CAP = 1 : 2
Let ∠CAQ = x and ∠CAP = 2x
∴ x + 2x = 180°
⇒ 3x = 180°
⇒ x = 180°/3 = 60°
∴ ∠CAQ = 60° and ∠CAP = 120°
∵ PAQ is the tangent and AC is the chord of the circle.
∴ ∠ADC = ∠CAQ = 60°
Similarly,
∠ABC = ∠CAP = 120°
Hence ∠A = 90° , ∠B = 120°
∠C = 90° and ∠D = 60°
Question 26. In a triangle ABC, the incircle (centre O) touches BC, CA and AB at P, Q and R respectively. Calculate (i) ∠QOR (ii) ∠QPR given that ∠A = 60°.
Answer :
OQ and OR are the radii and AC and AB are tangents.
OQ ⊥ AC and OR ⊥ AB
Now in the quad. AROQ
∠A = 60°, ∠ORA = 90° and ∠OQA = 90°
∴ ∠ROQ = 360° – (∠A + ∠ORA + ∠OQA)
= 360° – (60° + 90° + 90°)
= 360° – 240° = 120°
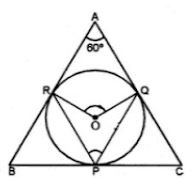
Now, arc RQ subtends ∠ROQ at the centre and ∠RPQ at the remaining part of the circle.
∴ ∠ROQ = 2∠RPQ
⇒ ∠RPQ = 1/2∠ROQ
⇒ ∠RPQ = ½ ∠ROQ
∠RPQ = ½ × 120°
= 60°
Question 27.
(a) In the figure (0 given below, AB is a diameter. The tangent at C meets AB produced at Q, ∠CAB = 34°. Find
(i) ∠CBA (ii) ∠CQA (2006)
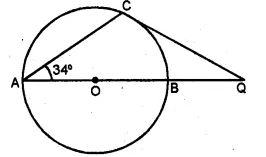
(b) In the figure (ii) given below, AP and BP are tangents to the circle with centre O. Given ∠APB = 60°, calculate.
(i) ∠AOB (ii) ∠OAB (iii) ∠ACB.
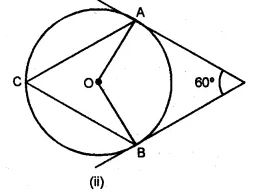
Answer :
(a) AB is the diameter.
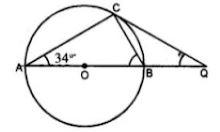
∴ ∠ACB = 90° and ∠CAB = 34°
∴ In ΔABC,
∠ACB + ∠CAB + ∠CBA = 180°
⇒ 90° + 34° + ∠CBA = 180°
(b) (i) AP and BP are the tangents to the circle and OA and OB are radii on it.
∴ OA ⊥ AP and OB ⊥ BP
∴ ∠AOB = 180° – 60° = 120°
(ii) Now in ΔOAB,
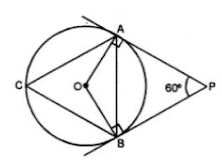
OA = OB (radii of the same circle)
∴ ∠OAB = ∠OBA
= ½ (180° – 120°)
= ½ × 60°
= 30°
(iii) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴ ∠AOB = 2∠ACB
⇒ ∠ACB = ½ ∠AOB
⇒ ∠ACB = ½ × 120°
= 60° [From (i)]
Question 28.
(a) In the figure (i) given below, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY. (1994)

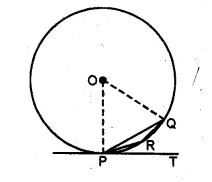
(b) In the figure (ii) given below, O is the centre of the circle and PT is the tangent to the circle at P. Given ∠QPT = 30°, calculate (i) ∠PRQ (ii) ∠POQ.
Answer :
(a) Join OY, OX and OY are the radii of the circle
and XT and YT are the tangents to the circle.

∴ OX ⊥ XT and OY ⊥ YT
and ∠XYT = 80°
∴ ∠XOY = 180° – ∠XTY
= 180° – 80°
Now ∠ZOY = 360° – (∠XOZ + ∠XOY)
= 360° – (140° + 100°)
= 360° – 240°
= 120°
But arc ZY subtends ∠ZOY at the centre and ∠ZXY at the remaining part of the circle.
∴ ∠ZXY = 1/2∠ZOY
= ½ × 120°
= 60°
(b) (i) PT is tangent and OP is radius, then OP ⊥ PT.

∴ ∠OPT = 90°
But ∠QPT = 30°
∴ ∠OPQ = 90° – 30°
= 60°
∵ OP = OQ (radii of the same circle)
∴ ∠OQP = ∠OPQ = 60°
Hence in ΔOPQ,
∠POQ = 60°
(ii) Tale a point A on the circumference and join AP and AQ.
Now arc PQ subtends ∠POQ at the centre and ∠PAQ on the circumference of the circle.
∴ ∠PAQ = 1/2∠POQ
= ½ × 60°
= 30°
Now APRQ is a cyclic quadrilateral.
∴ ∠PAQ + ∠PRQ = 180°
⇒ 30° + PRQ = 180°
⇒ 30° + ∠PRQ = 180°
⇒ ∠PRQ = 180° – 30°
= 150°
Question 29. Two chords AB, CD of a circle intersect internally at a point P.
(i) AP = cm, PB = 4 cm and PD = 3 cm, find PC.
(ii) AB = 12 cm, AP = 2 cm, PC = 5 cm, find PD.
(iii) AP = 5 cm, PB = 6 cm and CD = 13 cm, find CP.
Answer :
In a circle, two chords AB and CD intersect each other at P internally.
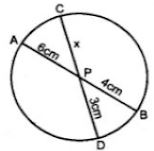
∴ AP.PB = CP.PD
(i) When AP = 6 cm, PB = 4 cm, PD = 3 cm,
Then
⇒ 6 × 4 = CP × 3
⇒ CP = (6 × 4)/3 = 8 cm
Hence PC = 8 cm
(ii) When AB = 12 cm, AP = 2 cm, PC = 5 cm
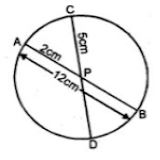
PB = AB – AP
= 12 – 2
= 10 cm
∵ AP × PB = CP × PD
⇒ 2 × 10 = 5 × PD
⇒ PD = (2 × 10)/5 = 4 cm
(iii) When AP = 5 cm, PB = 6 cm, CD = 13 cm
Let CP = x, then PD = CD – CP
Or PD = 13 – x
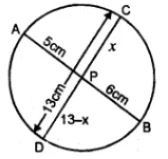
∴ AP × PB = CP × PD
⇒ 5 × 6 = x (13 – x)
⇒ 30 = 13x – x2
⇒ x2 – 13x + 30 = 0
⇒ x2 – 10x – 3x + 30 = 0
⇒ x(x – 10) – 3(x – 10) = 0
⇒ (x – 10)(x – 3) = 0
Either x – 10 = 0, then x = 10
Or x – 3 = 0, then x = 3
∴ CP = 10 cm or 3 cm
Question 30.
(a) In the figure (i) given below, PT is a tangent to the circle. Find TP if AT = 16 cm and AB = 12 cm.
(b) In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find (i) AB. (ii)the length of tangent PT.
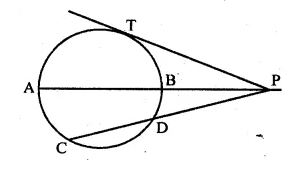
Answer :
(a) PT is the tangent to the circle and AT is a secant.
PT² = TA × TB
Now TA = 16 cm, AB = 12 cm
TB = AT – AB = 16 – 12 = 4 cm
∴ PT² = 16 + 4 = 64 = (8)²
⇒ PT = 8 cm or TP = 8 cm
(b) PT is tangent and PDC is secant out to the circle
∴ PT² = PC × PD
⇒ PT2 = (5 + 7.8) × 5 = 12.8×5
⇒ PT2 = 64
⇒ PT = 8 cm
In ΔOTP,
PT2 + OT2 = OP2
⇒ 82 + x2 = (x + 4)2
⇒ 64 + x2 = x2 + 16 + 8x
⇒ 64 – 16 = 8x
⇒ 48 = 8x
⇒ x = 48/8 = 6 cm
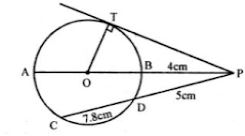
∴ Radius = 6 cm
AB = 2 × 6 = 12 cm
Circles Exe-15.3
ML Aggarwal Class 10 ICSE Maths Solutions
(Page 367)
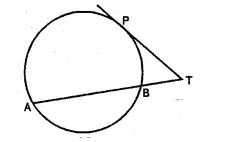
Question 31. PAB is secant and PT is tangent to a circle
(i) PT = 8 cm and PA = 5 cm, find the length of AB.
(ii) PA = 4.5 cm and AB = 13.5 cm, find the length of PT.
Answer :
∵ PT is the tangent and PAB is the secant of the circle.

∴ PT2 = PA.PB
(i) PT = 8 cm, PA = 5 cm
∴ (8)2 = 5 × PB
⇒ 64 = 5 PB
⇒ PB = 64/5 = 12.8 cm
∴ AB = PB – PA
= 12.8 – 5.0
= 7.8 cm
(ii) PT2 = PA × PB
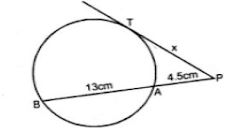
But PA = 4.5 cm, AB = 13.5 cm
∴ PB = PA + AB
= 4.5 + 13.5
= 18 cm
Now PT2 = 4.5 × 18
= 81
= (9)2
∴ PT = 9 cm.
Question 32. In the adjoining figure, CBA is a secant and CD is tangent to the circle. If AB = 7 cm and BC = 9 cm, then
(i) Prove that ∆ACD ~ ∆DCB.
(ii) Find the length of CD.
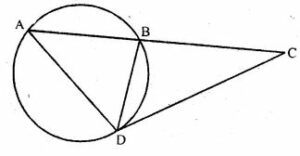
Answer :
In ∆ACD and ∆DCB
∠C = ∠C (common)
∠CAD = ∠CDB
∴ ΔACD ~ ΔDCB
∴ AC/DC = DC/BC
⇒ DC2 = AC × BC
= 16 × 9
= 144
⇒ DC = 12 cm
Question 33
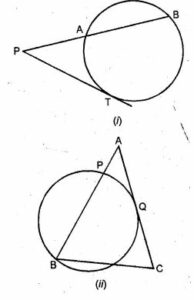
(a) In the figure (i) given below, PAB is secant and PT is tangent to a circle. If PA : AB = 1:3 and PT = 6 cm, find the length of PB.
(b) In the figure (ii) given below, ABC is an isosceles triangle in which AB = AC and Q is mid-point of AC. If APB is a secant, and AC is tangent to the circle at Q, prove that AB = 4 AP.
Answer :
(a) In the figure (i),
PAB is secant and PT is the tangent to the circle.
PT² = PA × PB
But PT = 6 cm, and PA : AB = 1 : 3
Let PA = x, then AB = 3x
∴ PB = PA + AB
= x + 3x
= 4x
Now PT2 = PA × PB
⇒ (6)2 = x(4x)
⇒ 36 = 4x2
⇒ x2 = 36/4 = 9
= (3)2
⇒ x = 3
∴ PB = 4x
= 4 × 3
= 12 cm
(b) In the figure (ii)
ΔABC is an isosceles triangles in which AB = AC
Q is mid-point of AC.
APB is the secant and AC is the tangent to the circle at Q.
To prove: AB = 4 AP
Proof :
∵ AQ is the tangent and APB is the secant.
∴ AQ2 = AP × AB
(1/2 AC)2 = AP × AB
⇒ (1/2 AB)2 = AP × AB (∵AB = AC)
⇒ AB2/4 = AP × AB
⇒ AB2 = 4AP × AB
⇒ AB2/AB = 4 AP
⇒ AB = 4 AP
Hence, proved.
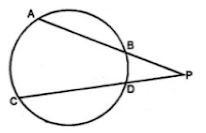
Question 34. Two chords AB, CD of a circle intersect externally at a point P. If PA = PC, Prove that AB = CD.
Answer :
Given: Two chords AB and CD intersect each other at P outside the circle. PA = PC.
To prove: AB = CD
Proof: Chords AB and CD intersect each other at P outside the circle.
∴ PA×PB = PC×PD
But PA = PC (given) …(i)
∴ PB = PD …(ii)
Substracting (ii) from (i)
PA – PB = PC – PD
⇒ AB = CD Q.E.D.
Question 35.
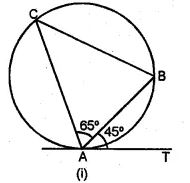
(a) In the figure (i) given below, AT is tangent to a circle at A. If ∠BAT = 45° and ∠BAC = 65°, find ∠ABC.
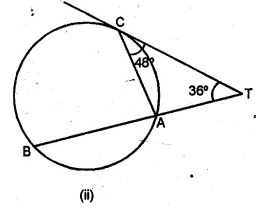
(b) In the figure (ii) given below, A, B and C are three points on a circle. The tangent at C meets BA produced at T. Given that ∠ATC = 36° and ∠ACT = 48°, calculate the angle subtended by AB at the centre of the circle. (2001)
Answer “
(a) AT is the tangent to the circle at A
and AB is the chord of the circle.
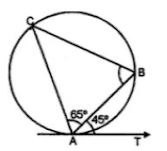
∴ ∠ACB = ∠BAT (Angles in the alternate segment)
= 45°
Now in ΔABC,
∠ABC + ∠BAC + ∠ACB = 180° (Angles of a triangle)
⇒ ∠ABC + 65° + 45° = 180°
⇒ ∠ABC + 110° = 180°
∴ ∠ABC = 180° – 110°
= 70°
(b) Join OA, OB and CB. In ΔATC,
Ext.∠CAB = ∠ATC + ∠TCA
= 36° + 48°
= 84°
But ∠TCA = ∠ABC (Angles in the alternate segment)
∴ ∠ABC = 48°
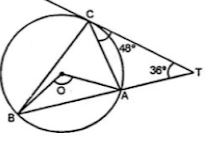
But in ΔABC,
∠ABC + ∠BAC + ∠ACB = 180°
⇒ 48° + 84° + ∠ACB = 180°
⇒ 132° + ∠ACB = 180°
⇒ ∠ACB = 180° – 132°
⇒ ∠ACB = 48°
∵ Arc. AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴ ∠AOB = 2∠ACB
= 2 × 48°
= 96°
Circles Exe-15.3
ML Aggarwal Class 10 ICSE Maths Solutions
(Page 368)
Question 36. In the adjoining figure ∆ABC is isosceles with AB = AC. Prove that the tangent at A to the circumcircle of ∆ABC is parallel to BC.
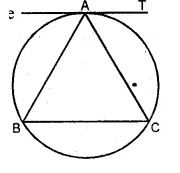
Answer :
Given: ∆ABC is an isosceles triangle with AB = AC.
AT is the tangent to the circumcircle at A.
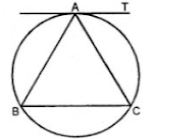
To prove: AT || BC.
Proof:
In ΔABC,
AB = AC (given)
∴ ∠C = ∠B (Angles opposite to equal sides)
But AT is the tangent and AC is the chord.
∴ ∠TAC = ∠B (Angles in the alternate segment)
But ∠B = ∠C (proved)
∴ ∠TAC = ∠C
But these are alternate angles
∴ AT || BC Q.E.D.
Question 37. If the sides of a rectangle touch a circle, prove that the rectangle is a square.
Answer :
Given: A circle touches the sides AB, BC, CD and DA
of a rectangle ABCD at P, Q, R and S respectively.
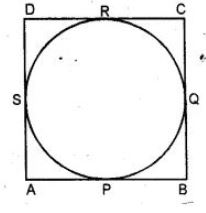
To prove: ABCD is a square.
Proof:
Tangents from a point to the circle are equal.
∴ AP = AS
Similarly BP = BQ
CR = CQ and DR = DS
Adding, we get
AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ AP + BP + CR + DR = AS + DS + BQ + CQ
⇒ AB + CD = AD + BC
But AB = CD and AD = BC (Opposite sides of a rectangle)
∴ AB + AB = BC + BC
⇒ 2 AB = 2 BC
⇒ AB = BC
∴ AB = BC = CD = DA
Hence, ABCD is a square.
Question 38
(a) In the figure (i) given below, two circles intersect at A, B. From a point P on one of these circles, two line segments PAC and PBD are drawn, intersecting the other circle at C and D respectively. Prove that CD is parallel to the tangent at P.
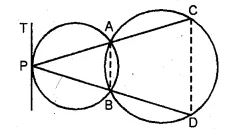
(b) In the figure (ii) given below, two circles with centers C, C’ intersect at A, B and the point C lies on the circle with centre C’. PQ is a tangent to the circle with centre C’ at A. Prove that AC bisects ∠PAB.

Answer :
Given: Two circles intersect each other at A and B.
From a point P on one circle, PAC and PBD are drawn.
From P, PT is a tangent drawn. CD is joined.

To prove : PT || CD.
Construction: Join AB.
Proof:
PT is tangent and PA is chord.
∴ ∠APT = ∠ABP (Angles in the alternate segments) …(i)
But BDCA is a cyclic quadrilateral
∴ Ext. ∠ABP = ∠ACD …(ii)
From (i) and (ii)
∠APT = ∠ACD
But these are alternate angles
∴ CD || PT
(b) Given : Two circles with centres C and C’ intersect each other at A and B. PQ is a tangent to the circle with centre C’ at A.
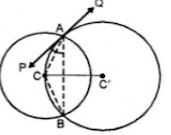
To Prove: AC bisects ∠PAB.
Construction: Join AB and CP.
Proof:
In ΔACB,
AC = BC (radii of the same circle)
∴ ∠BAC = ∠ABC …(i)
PAQ is tangent and AC is the chord of the circle.
∠PAC = ∠ABC …(ii)
From (i) and (ii)
∠BAC = ∠PAC
Hence, AC is the bisector of ∠PAB
Question 39.
(a) In the figure (i) given below, AB is a chord of the circle with centre O, BT is tangent to the circle. If ∠OAB = 32°, find the values of x and y.

(b) In the figure (ii) given below, O and O’ are centers of two circles touching each other externally at the point P. The common tangent at P meets a direct common tangent AB at M. Prove that:
(i) M bisects AB (ii) ∠APB = 90°.

Answer :
AB is a chord of a circle with centre O.
BT is a tangent to the circle and ∠OAB = 32°.
∴ In ∆OAB,
OA = OB (radii of the same circle)

∴ ∠OAB = ∠OBA
∴ x = 32°
And ∠AOB = 180°- (x + 32°)
= 180° – 64°
= 116°
Now, arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∠AOB = 2∠ACB
⇒ ∠ACB = 1/2∠AOB
= ½ × 116°
= 58°
Thus, x= 32° and y = 58°
(b) Given: Two circles with centre O and O’ touch each other at P externally. From P, a common tangent is drawn and meets the common direct tangent AB at M.

To prove : (i) M bisects AB i.e., AM = MB.
(ii) ∠APB = 90°
Proof :
(i) From M, MA and MP are the tangents.
∴ MA = MP …(i)
Similarly,
MB = MP …(ii)
From (i) and (ii)
MA = MB
Or, M is the mid-point of AB.
(ii) ∠MAP + ∠MPB = ∠MPA + MPB
⇒ ∠APB = ∠MAP + MBP
But ∠APB + ∠MAP + ∠MBP = 180°(Angles of a triangle)
⇒ ∠APB + ∠APB = 180°
⇒ 2∠APB = 180°
⇒ ∠APB = 180°/2
= 90°
— : End of ML Aggarwal Circles Exe-15.3 Class 10 ICSE Maths Solutions : –
Return to: ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends




