Friction HC Verma Exercise Questions Solutions Ch-6 Concept of Physics Vol-1 for ISC Class-11. Step by Step Solution of Exercise Questions of Ch-6 Friction HC Verma Concept of Physics . Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
Friction Exercise Questions Solutions HC Verma Ch-6 Concept of Physics Vol-1 for ISC Class-11
| Board | ISC and other board |
| Publications | Bharti Bhawan Publishers |
| Ch-6 | Friction |
| Class | 11 |
| Vol | 1st |
| writer | H C Verma |
| Book Name | Concept of Physics |
| Topics | Solution of Exercise Questions |
| Page-Number | 97, 98, 99 |
-: Select Topics :-
Exercise
Friction Exercise Questions Solutions
(HC Verma Ch-6 Concept of Physics Vol-1 for ISC Class-11)
Page-97
Question-1 :-
A body slipping on a rough horizontal plane moves with a deceleration of 4.0 m/s2. What is the coefficient of kinetic friction between the block and the plane?
Answer-1 :-
Let m be the mass of the body.
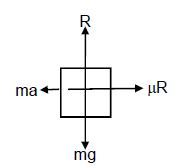
From the free body diagram,
R − mg = 0
(where R is the normal reaction force and g is the acceleration due to gravity)
⇒ R = mg (1)
Again ma − μkR = 0
(where μk is the coefficient of kinetic friction and a is deceleration)
or ma = μkR
From Equation (1),
ma = μkmg
⇒ a = μkg
⇒ 4 = μkg
⇒ 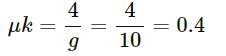
Hence, the coefficient of the kinetic friction between the block and the plane is 0.4 .
Question-2 :-
A block is projected along a rough horizontal road with a speed of 10 m/s. If the coefficient of kinetic friction is 0.10, how far will it travel before coming to rest?
Answer-2 :-
Let the deceleration be ‘a’.
Using free body diagram
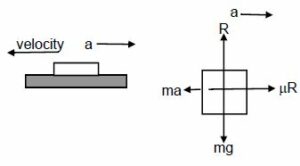
(where R is the normal reaction force)
⇒ R = mg ……. (1)
Again, ma − μkR = 0
(where μk is the coefficient of kinetic friction)
From Equation ….. (1),
⇒ ma = μkmg
⇒ a = μkg = 0.1 × 10
= 1 m/s2
Given:
initial velocity, u = 10 m/s
final velocity, v = 0 m/s (block comes to rest)
a = −1 m/s2 (deceleration)
Using equation of motion v2 – u2 = 2as
(where s is the distance travelled before coming to rest)
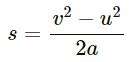
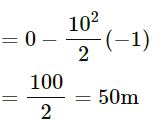
Therefore, the block will travel 50 m before coming to rest.
Question-3 :- (Friction HC Verma Exercise)
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ, find the frictional force acting on the block.
Answer-3 :-
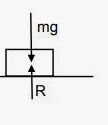
So, friction force is equal to the applied force. One of the case is that the friction force is equals to zero when the applied force is equal to zero.
Question-4 :-
A block slides down an inclined surface of inclination 30° with the horizontal. Starting from rest it covers 8 m in the first two seconds. Find the coefficient of kinetic friction between the two.
Answer-4 :-
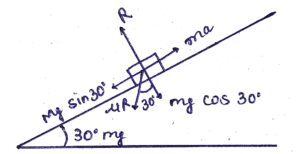
From the above diagram:
R − mg cos θ = 0
⇒ R = mg cos θ (1)
For the block, u = 0 m/s, s = 8 m and t = 2 s.
According to the equation of motion
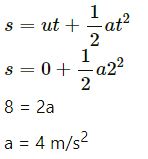
Again,
μkR + ma − mg sin θ = 0
(where μk is the coefficient of kinetic friction)
From Equation (1):
μkmg cos θ + ma − mg sin θ = 0
⇒ m (μkg cos θ + a − g sin θ) = 0
⇒ μk × 10 × cos 30° = g sin 30° − a
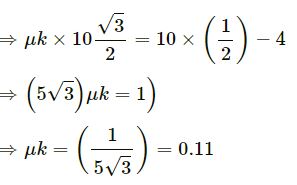
Therefore, the coefficient of kinetic friction between the block and the surface is 0.11.
Question-5 :- (Friction HC Verma Exercise)
Suppose the block of the previous problem is pushed down the incline with a force of 4 N. How far will the block move in the first two seconds after starting from rest? The mass of the block is 4 kg.
Answer-5 :-
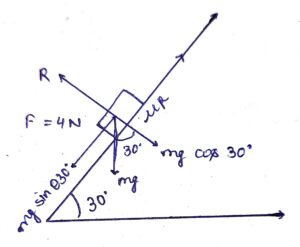
From the above diagram:
F − ma − μkR + mg sin 30° = 0
4 − 4a − μkR + 4g sin 30° = 0 (1)
R − 4g cos 30° = 0 (2)
⇒ R = 4g cos 30° = 0
Substituting the values of R in Equation (1) we get
4 − 4a − 0.11 × 4g cos 30° + 4g sin 30° = 0
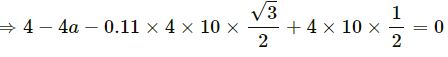
4 − 4a − 3.18 + 20 = 0
a ≈ 5 m/s2
For the block, u = 0, t = 2 s and a = 5 m/s2.
According to the equation of motion,
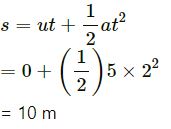
Therefore, the block will move 10 m.
Question-6 :-
A body of mass 2 kg is lying on a rough inclined plane of inclination 30°. Find the magnitude of the force parallel to the incline needed to make the block move (a) up the incline (b) down the incline. Coefficient of static friction = 0.2.
Answer-6 :-
Applied force = μR + 2g sin 30° (1)
(where μ is the coefficient of static friction)
R = mg cos 30°
Substituting the respective values in Equation (1), we get
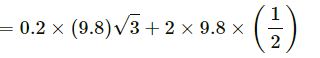

(b) Net force acting down the incline is given by
F = 2g sin 30° − μR
= 6.41 N
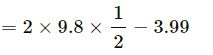
Because F = 6.41 N, the body will move down the incline with acceleration, hence the force required is zero.
Question-7 :-
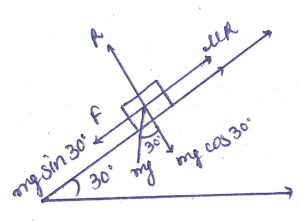
Repeat part (a) of problem 6 if the push is applied horizontally and not parallel to the incline.
Answer-7 :-
Using the free body diagram,

g = 10 m/s2, m = 2 kg, θ = 30 and μ = 0.2
R − mg cos θ − F sin θ = 0
⇒ R = mg cos θ + F sin θ (1)
and
mg sin θ + μR − F cos θ = 0
⇒ mg sin θ + μ(mg cos θ + F sin θ) − F cos θ = 0
⇒ mg sin θ + μmg cos θ + μF sin θ − F cos θ = 0
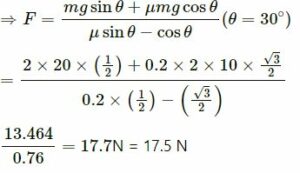
Therefore, while pushing the block to move up on the incline, the required force is 17.5 N.
Question-8 :- (Friction HC Verma Exercise)
In a children-park an inclined plane is constructed with an angle of incline 45° in the middle part (in the following figure). Find the acceleration of boy sliding on it if the friction coefficient between the cloth of the boy and the incline is 0.6 and g = 19 m/s2.
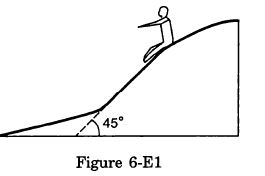
Answer-8 :-
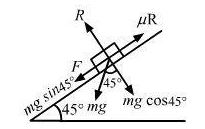
R − mg cos 45° = 0
R = mg cos 45° =mg/√2 …………. (1)
Net force acting on the boy, making him slide down
= mg sin 45° − μR
= mg sin 45° − μmg cos 45°
Question-9 :-
A body starts slipping down an incline and moves half metre in half second. How long will it take to move the next half metre?
Answer-9 :-
Let a be the acceleration of the body sliding down.
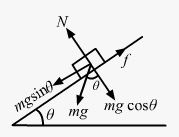
From the above diagram:
R − mg cos θ = 0
⇒ R = mg cos θ (1)
and
ma + mg sin θ − μR = 0
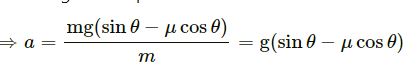
For the first half metre, u = 0, s = 0.5 m and t = 0.5 s.
According to the equation of motion,
v = u + at
= 0 + (0.5)4 = 2 m/s
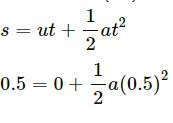
⇒ a = 4 m/s2
For the next half metre, u = 2 m/s, a = 4 m/s2 and s = 0.5.

Therefore, the time taken to cover the next half metre is 0.21 s
Question-10 :-
The angle between the resultant contact force and the normal force exerted by a body on the other is called the angle of friction. Show that, if λ be the angle of friction and μ the coefficient of static friction λ ≤ tan−1 μ.
Answer-10 :-
f be the applied force,
R be the normal reaction force and
F be the frictional force.

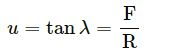
(where λ is the angle of friction)
When F = μR, F is the limiting friction (maximum friction). When applied force increases and the body still remains still static then the force of friction increases up to its maximum value equal to limiting friction (μR).
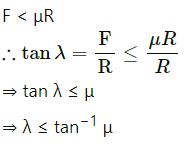
Question-11 :- (Friction HC Verma Exercise)
Consider the situation shown in the following figure. Calculate (a) the acceleration of the 1.0 kg blocks, (b) the tension in the string connecting the 1.0 kg blocks and (c) the tension in the string attached to 0.50 kg.
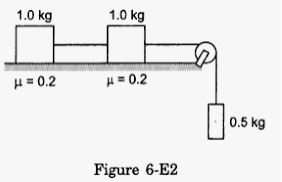
Answer-11 :-
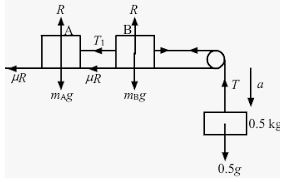
From the above diagrams:
T + ma − mg = 0
T + 0.5a − 0.5 g = 0 (1)
μR + ma + T1 − T = 0
μR + 1a + T1 − T = 0 (2)
μR + 1a − T1 = 0
μR + a = T1 (3)
From Equations (2) and (3) we have
μR + a = T − T1
⇒ T − T1 = T1
⇒ T = 2T1
So, Equation (2) becomes
μR + a + T1 − 2T1 = 0
⇒ μR + a − T1 = 0
⇒ T1 = μR + a
= 0.2g + a (4)
and Equation (1) becomes
2T1 + 0.5a − 0.5g = 0

= 0.25g – 0.25a (5)
From Equations (4) and (5)
0.2g + a = 0.25g − 0.25a
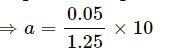
= 0.4 x 10 m/s2 [g = 10 m/s2]
Therefore,
(a) the acceleration of each 1 kg block is 0.4 m/s2,
(b) the tension in the string connecting the 1 kg blocks is
T1 = 0.2g + a + 0.4 = 2.4 N
and
(c) the tension in the string attached to the 0.5 kg block is
T = 0.5g − 0.5a
= 0.5 × 10 − 0.5 × 0.4
= 4.8 N.
Question-12 :-
If the tension in the string in the following figure is 16 N and the acceleration of each block is 0.5 m/s2, find the friction coefficients at the two contact with the blocks.
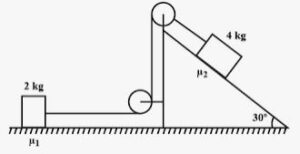
Answer-12 :-
From the free body diagram:
μ1R + m1a − F = 0
μ1R + 1 − 16 = 0 (R = mg cos θ)
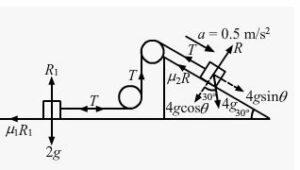

Therefore, the friction coefficients at the two contacts with blocks are μ1 = 0.75 and μ2 = 0.06.
Question-13 :-
The friction co-efficient between the table and the block shown in the following figure is 0.2. Find the tensions in the two strings.
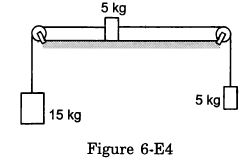
Answer-13 :-

From the above diagram,
T + m1a − m1g = 0
T + 15a − 15g = 0
⇒ T = 15g − 15a (1)
Now,
T1 − m2g − m2a = 0
T1 − 5g − 5a = 0
⇒ T1 = 5g + 5a (2)
Again,
T − (T1 + 5a + m2R) = 0
⇒ T − (5g + 5a + 5a +m2R) = 0 (3)
(where R = μg)
From Equations (1) and (2),
15g − 15a = 5g + 10a + 0.2 (5g)
⇒ 25a = 90 [g = 10 m/s2]
⇒ a = 3.6 m/s2
From Equation (3),
T = 5 × 10 + 10 × 3.6 + 0.2 × 5 × 10 = 96 N in the left string.
From Equation (2),
T1 = 5g + 5a
= 5 × 10 + 5 × 36
= 50 + 18
= 68 N in the right string.
Question-14 :-
The friction coefficient between a road and the type of a vehicle is 4/3. Find the maximum incline the road may have so that once had brakes are applied and the wheel starts skidding, the vehicle going down at a speed of 36 km/hr is stopped within 5 m.
Answer-14 :-
Given,
initial velocity of the vehicle, u = 36 km/h = 10 m/s
final velocity of the vehicle, v = 0
s = 5m, μ = 4/3, g = 10 m/s2
Let the maximum angle of incline be θ.
Using the equation of motion
From the free body diagram
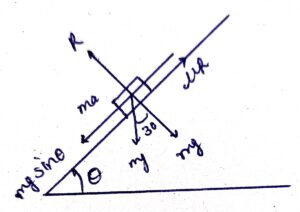
R − mg cos θ = 0
⇒ R = mg cos θ (1)
Again,
ma + mg sin θ − μ R = 0
⇒ ma + mg sin θ − μmg cos θ = 0
⇒ a + g sin θ − μg cos θ = 0

⇒ 30 + 30 sin θ − 40 cos θ = 0
⇒ 3 + 3 sin θ − 4 cos θ = 0
⇒ 4 cos θ − 3 sin θ = 3

Therefore, the maximum incline of the road, θ = 16°.
Question-15 :- (Friction HC Verma Exercise)
The friction coefficient between an athelete’s shoes and the ground is 0.90. Suppose a superman wears these shoes and races for 50 m. There is no upper limit on his capacity of running at high speeds. (a) Find the minimum time that he will have to take in completing the 50 m starting from rest. (b) Suppose he takes exactly this minimum time to complete the 50 m, what minimum time will he take to stop?
Answer-15 :-
To reach the 50 m distance in minimum time, the superman has to move with maximum possible acceleration.
Suppose the maximum acceleration required is ‘a’.
∴ ma − μR = 0 ⇒ ma = μ mg
⇒ a = μg = 0.9 × 10 = 9 m/s2
(a) As per the question, the initial velocity,
u = 0, t = ?
a = 9 m/s2, s = 50 m
From the equation of motion,
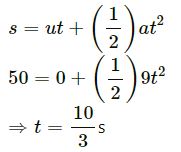
(b) After covering 50 m, the velocity of the athelete is
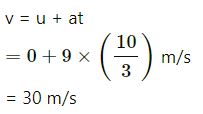
The superman has to stop in minimum time. So, the deceleration, a = − 9 m/s2 (max)
R = mg
ma = μR (maximum frictional force)
ma = μmg
⇒ a = μg
= 9 m/s2 (deceleration)
u1 = 30 m/s, v = 0
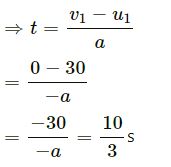
Question-16 :-
A care is going at a speed of 21.6 km/hr when it encounters at 12.8 m long slope of angle 30° (in the following figure). The friction coefficient between the road and the tyre is 1/2√3. Show that no matter how hard the driver applies the brakes, the car will reach the bottom with a speed greater than 36 km/hr. Take g = 10 m/s2.
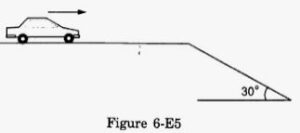
Answer-16 :-
When the driver applies hard brakes, it signifies that maximum force of friction is developed between the tyres of the car and the road.
So, maximum frictional force = μR
From the free body diagram,
R − mg cos θ = 0
⇒ R = mg cos θ (1)
and
μR + ma − mg sin θ = 0 (2)
⇒ μ mg cos θ + ma − mg sin θ = 0
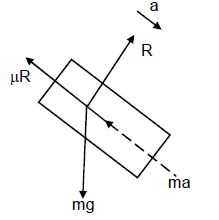
where θ = 30˚
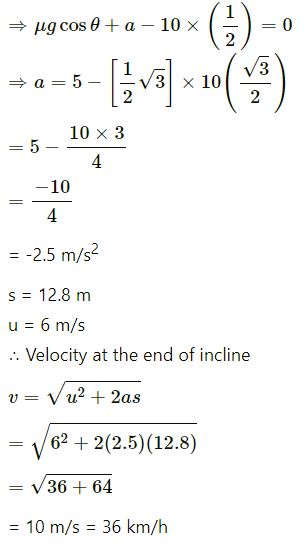
Therefore, the harder the driver applies the brakes, the lower will be the velocity of the car when it reaches the ground, i.e. at 36 km/h.
Question-17 :-
A car starts from rest on a half kilometre long bridge. The coefficient of friction between the tyre and the road is 1.0. Show that one cannot drive through the bridge in less than 10 s.
Answer-17 :-
Let a be the maximum acceleration of the car for crossing the bridge.
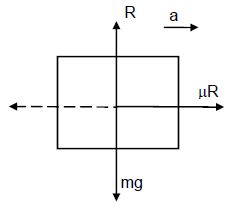
From the above diagram,
ma = μR
(For more accelerations the tyres will slip)
ma = μmg
a = μg = 1 × 10 = 10 m/s2
To cross the bridge in minimum possible time, the car must be at its maximum acceleration.
u = 0, s = 500 m, a = 10 m/s2
From the equation of motion,
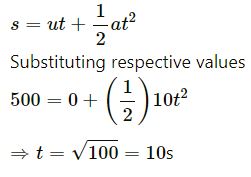
Therefore, if the car’s acceleration is less than 10 m/s2, it will take more than 10 s to cross the bridge. So, one cannot drive through the bridge in less than 10 s.
Question-18 :- (Friction HC Verma Exercise)
In the following figure shows two blocks in contact sliding down an inclined surface of inclination 30°. The friction coefficient between the block of mass 2.0 kg and the incline is μ1, and that between the block of mass 4.0 kg and incline is μ2. Calculate the acceleration of the 2.0 kg block if (a) μ1 = 0.20 and μ2 = 0.30, (b) μ1 = 0.30 and μ2 = 0.20. Take g = 10 m/s2.
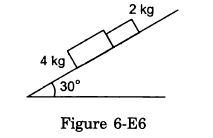
Answer-18 :-

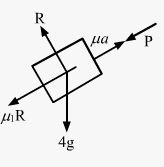

μ2R + 4a − p − 4g sin 30° = 0
⇒ 0.3 x (40) cos 30° + 4a − p − 40 sin 30° = 20 (2)
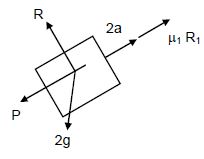
p + 2a − μ1R1 − 2g sin 30° = 0 (4)
From Equation (2),

= 2.69 = 2.7 m/s2
(b) In this case, the 4 kg block will move at a higher acceleration because the coefficient of friction is less than that of the 2 kg block. Therefore, the two blocks will move separately. By drawing the free body diagram of 2 kg mass, it can be shown that a = 2.4 m/s².
Question-19 :-
Two masses M1 and M2 are connected by a light rod and the system is slipping down a rough incline of angle θ with the horizontal. The friction coefficient at both the contacts is μ. Find the acceleration of the system and the force by the rod on one of the blocks.
Answer-19 :-
From the free body diagram
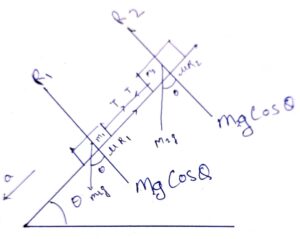
R1 = M1g cos θ (1)
R2 = M2g cos θ (2)
T + M1g sin θ − M1a − μR1 = 0 (3)
T − M2g + M2a + μR2 = 0 (4)
From Equation (3),
T + M1g sin θ − M1 a − μM1g cos θ = 0 (5)
From Equation (4),
T − M2 g sin θ + M2 a + μM2 g cos θ = 0 (6)
From Equations (5) and (6),
g sin θ(M1 + M2) − a(M1 + M2) − μg cos θ (M1 + M2)
⇒ a(M1 + M2) = g sin θ(M1 + M2) = μg cos θ (M1 + M2)
⇒ a = g(sin θ − μ cos θ)a − g(sin θ − μ cos θ)
∴ The acceleration of the block (system) = g(sin θ − μcos θ)
The force exerted by the rod on one of the blocks is tension, T.
T = −M1g sin θ + M1a + μM1g cos θ
T = −M1g sin θ + M1(g sin θ − μg cos θ) + μM1g cos θ = 0
Question-20 :-
A block of mass M is kept on a rough horizontal surface. The coefficient of static friction between the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
Answer-20 :-
Let P be the force applied to slide the block at an angle θ.
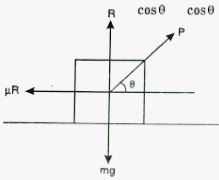
From the free body diagram,
R + P sin θ − mg = 0
⇒ R = −P sin θ + mg (1)
μR = P cos θ (2)
From Equation (1),
μ(mg − P sin θ)−P cos θ = 0
⇒ μmg = μP sin θ + P cos θ
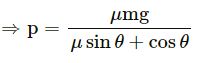
The applied force P should be minimum, when μ sin θ + cos θ is maximum.
Again, μ sin θ + cos θ is maximum when its derivative is zero:
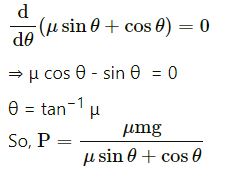
Dividing numerator and denominator by cos θ, we get
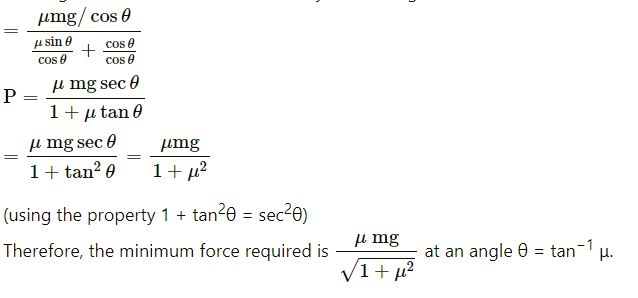
Question-21 :-
The friction coefficient between the board and the floor shown in the following figure is μ. Find the maximum force that the man can exert on the rope so that the board does not slip on the floor.
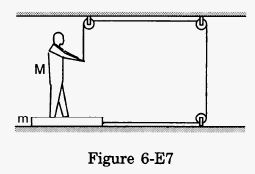
Answer-21 :-
Let T be the maximum force exerted by the man on the rope.
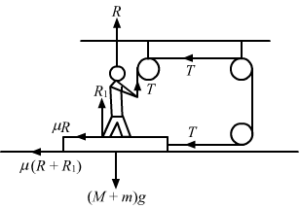
From the free body diagram,
R + T = Mg
⇒ R = Mg − T (1)
Again,
R1 − R − mg = 0
⇒ R1 = R + mg (2)
and
T − μR1 = 0
From Equation (2),
T − μ(R + mg) = 0
⇒ T − μR − μ mg = 0
⇒ T − μ(Mg − T) − μmg = 0
T − μMg + μt − μmg = 0

Question-22 :- (Friction HC Verma Exercise)
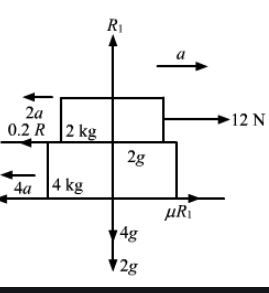
A 2 kg block is placed over a 4 kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the block is 0.20. Find the acceleration of the two blocks if a horizontal force of 12 N is applied to (a) the upper block, (b) the lower block. Take g = 10 m/s2.
Answer-22 :-

Consider the free body diagram.
(a) For the mass of 2 kg, we have:
R1 − 2g = 0
⇒ R1 = 2 × 10 = 20
2a + 0.2 R1 − 12 = 0
⇒ 2a + 0.2 (20) = 12
and⇒ 2a = 12 − 4
⇒ a = 4 m/s2
Now,
4a − μR1 = 0
⇒ 4a = μR1 = 0.2 (20) = 4
⇒ a1 = 1 m/s2

The 2 kg block has acceleration 4 m/s2 and the 4 kg block has acceleration 1 m/s2.
(ii) We have:
R1 = 2g = 20
Ma = μR1 = 0
a = 0
And,
Ma + μmg − F = 0
4a + 0.2 × 2 × 10 − 12 = 0
⇒ 4a + 4 = 12
⇒ 4a = 8
therefore⇒ a = 2 m/s2
Question-23 :-
Find the accelerations a1, a2, a3 of the three blocks shown in the following figure if a horizontal force of 10 N is applied on (a) 2 kg block, (b) 3 kg block, (c) 7 kg block. Take g = 10 m/s2.

Answer-23 :-
Given:
μ1 = 0.2, μ2 = 0.3 and μ3 = 0.4
from diagram, we have:

(a) When the 10 N force is applied to the 2 kg block, it experiences maximum frictional force.
Here,
μ1R1 = μ1 × m1g
μ1R1 = μ1 × 2g = (0.2) × 20
= 4 N (From the 3 kg block)
Net force experienced by the 2 kg block = 10 − 4 = 6 N
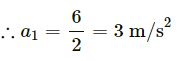
But for the 3 kg block (Fig. 3), the frictional force from the 2 kg block, i.e, 4 N, becomes the driving force and the maximum frictional force between the 3 kg and 7 kg blocks.
Thus, we have:
μ2 = R2 = μ2m2g = (0.3) × 5 kg
= 15 N
Therefore, the 3 kg block cannot move relative to the 7 kg block.
The 3 kg block and the 7 kg block have the same acceleration (a2 = a3), which is due to the 4 N force because there is no friction from the floor.
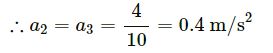
(b) When the 10 N force is applied to the 3 kg block, it experiences maximum frictional force of (15 + 4) N, i.e., 19 N, from the 2 kg block and the 7 kg block.
So, it cannot move with respect to them.
As the floor is frictionless, all the three bodies move together.
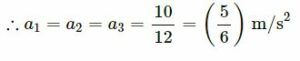
(c) Similarly, it can be proved that when the 10 N force is applied to the 7 kg block, all three blocks move together with the same acceleration.
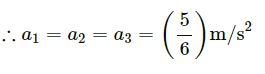
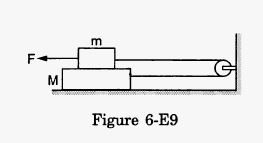
Question-24 :- (Friction HC Verma Exercise)
The friction coefficient between the two blocks shown in the following figure is μ but the floor is smooth. (a) What maximum horizontal force F can be applied without disturbing the equilibrium of the system? (b) Suppose the horizontal force applied is double of that found in part (a). Find the accelerations of the two masses.
Answer-24 :-
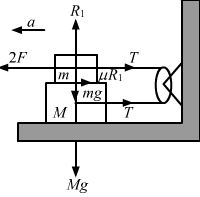
From the free body diagrams of the two blocks, we have
R1 = mg …(i)
F = μR1+T …(ii)
T − μR1 = 0 ..(iii)
From equations (i) and (ii), we have
F − μmg = T …(ii)
From equations (i) and (iii), we have
T = μmg
Putting T = μmg in equation (ii), we have
F = μmg + μmg = 2μmg

b) From the free body diagram of upper block, we have
2F − T − μmg = ma ….(i)
From the free body diagram of lower block, we have
T = Ma + μmg
Putting the value of T in (i), we get
2F − Ma − μmg − μmg = ma
Putting F = 2μmg, we get
2(2μmg) − 2μmg = a(M + m)
⇒ 4μmg − 2μmg = a(M + m)

Question-25 :-
Suppose the entire system of the previous questions is kept inside an elevator which is coming down with an acceleration a < g. Repeat parts (a) and (b).
Answer-25 :-
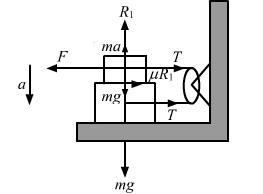
From the free body diagram, we have:
R1 + ma − mg = 0
⇒ R1 = m (g − a)
= mg − ma …(i)
Now,
F − T − μR1 = 0 and
T − μR1 = 0
⇒ F − [μ (mg − ma)] − μ(mg − ma) = 0
and⇒ F − μ mg − μma − μmg + μma = 0
⇒ F = 2 μmg − 2 μma
hence= 2 μm (g − a)
(b) Let the acceleration of the blocks be a1

R1 = mg − ma ….(i)
And,
2F −T − μR1 = ma1 …(ii)
Now,
T = μR1 + Ma1
= μmg − μma + Ma1
Substituting the value of F and T in equation (ii), we get:
2[2μm(g − a)] − (μmg − μma + Ma1) − μmg + μma = ma1
⇒ 4μmg − 4μma − 2μmg + 2μma= ma1 + Ma1
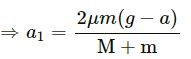
Thus, both the blocks move with same acceleration a1 but in opposite directions.
Question-26 :-
Consider the situation shown in the following figure. Suppose a small electric field E exists in the space in the vertically charge Q on its top surface. The friction coefficient between the two blocks is μ but the floor is smooth. What maximum horizontal force F can be applied without disturbing the equilibrium?
[Hint: The force on a charge Q bye the electric field E is F = QE in the direction of E.]

Answer-26 :-
From the diagram:

R1 + QE − mg = 0
where
R1 is the normal reaction force
Q is the charge
E is the small electric field
⇒ R1 = mg − QE (1)
F − T − μR1 = 0
F − T = μR1
where F is the maximum horizontal force required
From Equation (1),
F − T − μ(mg − QE) = 0
F − T = μ(mg − QE)
⇒ F − T − μmg + μQE = 0 (2)
T − μR1 = 0
⇒ T = μR1 = μ (mg − QE) (3)
From Equation (2),
F − μmg + μ QE − μmg + μQE = 0
⇒ F − 2 μmg + 2μQE = 0
and ⇒ F = 2μmg − 2μQE
⇒ F = 2μ (mg − QE)
Therefore, the maximum horizontal force that can be applied is 2μ (mg − QE).
Question-27 :-
A block of mass m slips on a rough horizontal table under the action of a horizontal force applied to it. The coefficient of friction between the block and the table is μ. The table does not move on the floor. Find the total frictional force applied by the floor on the legs of the table. Do you need the friction coefficient between the table and the floor or the mass of the table?
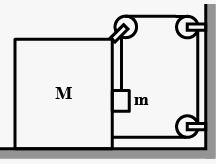
Answer-27 :-
R = mg
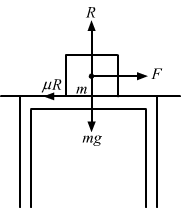
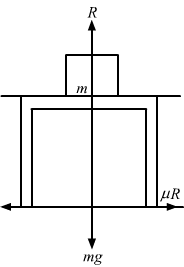
From the free body diagram,
F − μR = 0
⇒ F = μR = μmg
But the table is at rest, so the frictional force at the legs of the table is also μR. Let this be f, so from the free body diagram
f − μR = 0
⇒ f = μR = μmg
Therefore, the total frictional force on the table by the floor is μmg.
Question-28 :- (Friction HC Verma Exercise)
Find the acceleration of the block of mass M in the situation of figure in the following. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
Answer-28 :-
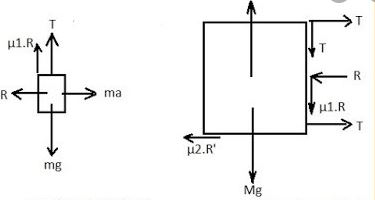
Let the acceleration of block of mass M is ‘a’ towards right. So, the block ‘m’ must go down with an acceleration ‘2a’.
As the block ‘m’ is in contact with the block ‘M’, it will also have acceleration ‘a’ towards right. So, it will experience two inertial forces as shown in figure (b). From free body diagram
R1 – ma = 0
⇒ R1 = ma (i)
Also,
2ma + T – Mg + μ1R1 = 0
⇒ T = Mg – (2 + μ1) ma (ii)
Using the free body diagram (c), we can write,
T + μ1R1 + Mg – R2 = 0
Substituting the value of R1 from (i), we get,
R2 = T + μ1 ma + mg
Substituting the value of T from (ii), we get,
R2 = (Mg – 2ma – μ1ma) = μ1 ma + Mg + ma
∴ R2 = Mg + Ma – 2ma ….(iii)
Again, using the free body diagrams (c),
T + T – R – Ma – μ2R2 = 0
⇒ 2T – Ma – ma – μ2(Mg + mg – 2ma) = 0
Substituting the values of R1 and R2 from (i) and (iii), we get:
2T = (M + m)a + μ2 (Mg + mg – 2ma) ….(iv)
From equations (ii) and (iv), we have:
2T = 2mg – 2(2 + μ1) ma
= (M + m) a + μ1(Mg + mg – 2ma)
⇒ 2mg – μ2 (M + m)g = a[M + m – 2μ2m + 4m + 2μ1m]
Therefore, the acceleration of the block of mass M in the given situation is given by
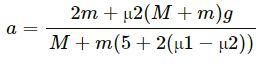
Question-29 :-
A block of mass 2 kg is pushed against a rough vertical wall with a force of 40 N, coefficient of static friction being 0.5. Another horizontal force of 15 N, is applied on the block in a direction parallel to the wall. Will the block move? If yes, in which direction? If no, find the frictional force exerted by the wall on the block.
Answer-29 :-
Net force on the block =√20²+152 – (0.5) × 40
= 25 – 20 = 5 N
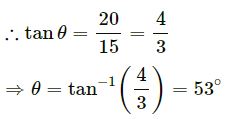
Therefore, the block will move at 53° angle with the 15 N force.
Question-30 :-
A person (40 kg) is managing to be at rest between two vertical walls by pressing one wall A by his hands and feet and the other wall B by his back (in the following figure). Assume that the friction coefficient between his body and the walls is 0.8 and that limiting friction acts at all the contacts. (a) Show that the person pushes the two wall with equal force. (b) Find the normal force exerted by either wall on the person. Take g = 10 m/s2.
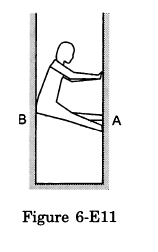
Answer-30 :-
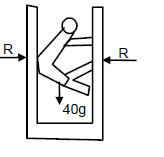
μR + μR = mg
⇒ 2μR = 40 × 10

Question-31 :- (Friction HC Verma Exercise)
In the following figure shows a small block of mass m kept at the left end of a larger block of mass M and length l. The system can slide on a horizontal road. The system is started towards right with an initial velocity v. The friction coefficient between the road and the bigger block is μ and that between the block is μ/2. Find the time elapsed before the smaller blocks separates from the bigger block.
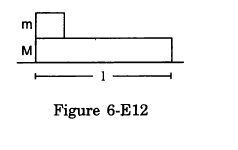
Answer-31 :-
Let a1 and a2 be the accelerations of masses m and M, respectively.
Also, a1 > a2 so that mass m moves on mass M.
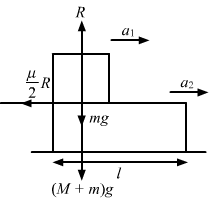
Let after time t, mass m is separated from mass M.
Using the equation of motion
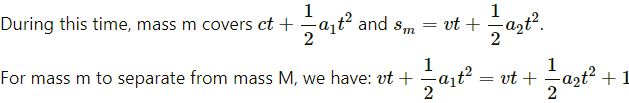
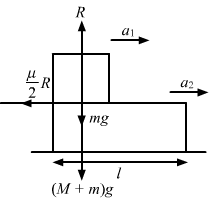
From the free body diagram, we have:
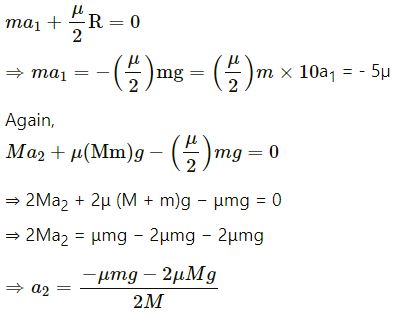
Substituting the values of a1 and a2 in equation (i), we get:
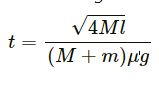
—: End of Friction Exercise Solutions Concept of Physics:–
Return to — HC Verma Solutions Vol-1 Concept of Physics
Thanks


