Friction Obj-1 HC Verma Solutions Vol-1 Chapter-6 Vol-1 Concept of Physics for Class-11. Step by Step Solutions of Objective -1 (MCQ-1) Questions of Chapter-6 Friction (Concept of Physics) .Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
Friction Obj-1 (MCQ-1) HC Verma Solutions Ch-6 Vol-1 Concept of Physics for Class-11
| Board | ISC and other board |
| Publications | Bharti Bhawan Publishers |
| Chapter-6 | Friction |
| Class | 11 |
| Vol | 1st |
| writer | HC Verma |
| Book Name | Concept of Physics |
| Topics | Solution of Objective-1 (MCQ-1) Questions |
| Page-Number | 96 |
-: Select Topics :-
Objective-I
Friction Obj-1 (MCQ-1) HC Verma
HC Verma Solutions of Ch-6 Vol-1 Concept of Physics for Class-11
(Page-96)
Question-1
In a situation the contact force by a rough horizontal surface on a body placed on it has constant magnitude. If the angle between this force and the vertical is decreased, the frictional force between the surface and the body will
(a) increase
(b) decrease
(c) remain the same
(d) may increase or decrease.
Answer-1
The option (b) decrease is correct
Explanation:

According to the first law of limiting friction,
f = μN
where f is the frictional force
N is the normal reaction force
μ is the coefficient of static friction
and
N = mg - Fcosθ
where m is the mass of the body
F is the contact force acting on the body
Question-2 :-
While walking on ice, one should take small steps to avoid slipping. This is because smaller steps ensure
(a) larger friction
(b) smaller friction
(c) larger normal force
(d) smaller normal force.
Answer-2:-
The option (b) smaller friction is correct
Explanation:
According to the first law of the limiting friction,
f = μN
where f is the frictional force
μ is the coefficient of friction
N is the normal reaction force
When we take smaller steps on ice, the normal reaction force exerted by the ice is small. Therefore, the smaller steps ensure smaller friction.
Question-3 :-
A body of mass M is kept on a rough horizontal surface (friction coefficient = μ). A person is trying to pull the body by applying a horizontal force but the body is not moving. The force by the surface on A is F, where
(a) F = Mg
(b) F = μ Mg
(c) Mg ≤ F ≤ Mg a √1+μ2
(d) Mg ≥ F ≥ Mg √1-μ2
Answer-3 :-
The option (c) Mg ≤ F ≤ Mg a √1+μ2 is correct
Explanation:
Let T be the force applied on an object of mass M.
If T = 0, F min = Mg.
If T is acting in the horizontal direction, then the body is not moving.
∴ T = μ(mg)
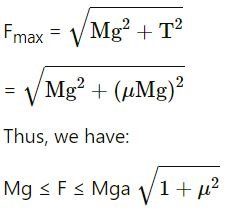
Question-4 :-
A scooter starting from rest moves with a constant acceleration for a time ∆t1, then with a constant velocity for the next ∆t2 and finally with a constant deceleration for the next ∆t3 to come to rest. A 500 N man sitting on the scooter behind the driver manages to stay at rest with respect to the scooter without touching any other part. The force exerted by the seat on the man is
(a) 500 N throughout the journey
(b) less than 500 N throughout the journey
(c) more than 500 N throughout the journey
(d) > 500 N for time ∆t1 and ∆t3 and 500 N for ∆t2.
Answer-4 :-
The option (d) > 500 N for time ∆t1 and ∆t3 and 500 N for ∆t2. is correct
Explanation:
During the time interval ∆t2, the scooter is moving with a constant velocity, which implies that the force exerted by the seat on the man is 500 N (for balancing the weight of the man).
During the time interval ∆t1 and ∆t3, the scooter is moving with constant acceleration and deceleration, which implies that a frictional force is also applied. Therefore, the net force exerted by the seat on the man should be >500 N.
Question-5 :-
Consider the situation shown in figure. The wall smooth but the surface of A and B in contact are rough. The friction on B due to A in equilibrium

(a) is upward
(b) is downward
(c) is zero
(d) the system cannot remain in equilibrium.
Answer-5 :-
The option (d) the system cannot remain in equilibrium. is correct
Explanation:

Since the wall is smooth and the surface of A and B in contact are rough, the net vertical force on the system is in the downward direction. Hence, the system cannot remain in equilibrium.
Question-6 :-
Suppose all the surface in the previous problem are rough. The direction of friction of B due to A
(a) is upward
(b) is downward
(c) is zero
(d) depends on the masses of A and B
Answer-6 :-
The option (a) is upward is correct
Explanation:
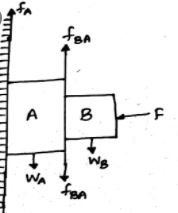
The normal reaction force on the system (comprising of wall and contact surface of A and B) is provided by F. As can be seen from the figure, the weight of A and B is in the downward direction. Therefore, the frictional force f A and f BA (friction on B due to A) is in upward direction.
Question-7 :-
Two cars of unequal masses use similar tyres. If they are moving at the same initial speed, the minimum stopping distance
(a) is smaller for the heavier car
(b) is smaller for the lighter car
(c) is same for both cars
(d) depends on the volume of the car
Answer-7 :-
The option (c) is same for both cars is correct
Explanation:
Given: both the cars have same initial speed.
Let the masses of the two cars be m1 and m2.
Frictional force on car with mass m1 = μm1 g
So, the deceleration due to frictional force =
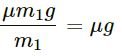
Frictional force on car with mass m2 = μm2 g
So, the deceleration due to frictional force

As both the acceleration are same, from the second equation of motion

Thus, we can say that both the cars have same minimum stopping distance.
Question-8 :-
In order to stop a car in shortest distance on a horizontal road, one should
(a) apply the brakes very hard so that the wheels stop rotating
(b) apply the brakes hard enough to just prevent slipping
(c) pump the brakes (press and release)
(d) shut the engine off and not apply brakes
Answer-8 :-
The option (b) apply the brakes hard enough to just prevent slipping is correct
Explanation:
Question-9 :-
A block A kept on an inclined surface just begins to slide if the inclination is 30°. The block is replaced by another block B and it is found that it just begins to slide if the inclination is 40°.
(a) mass of A > mass of B
(b) mass of A < mass of B
(c) mass of A = mass of B
(d) all of three are possible.
Answer-9 :-
The option (d) all of three are possible. is correct
Explanation:
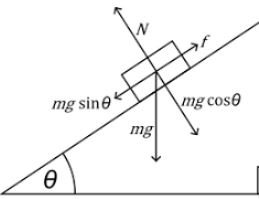
We know that
N = mg cos θ˚
f max = μN = μmg cos θ
where N = normal reaction force
f max = frictional force
θ = angle of inclination
μ = coefficient of friction
When the block just begins to slide, it means
mg sin θ = f max
mg sin θ = μmg cos θ
μ = tan θ
and the coefficient of friction depends on the angle of inclination (θ) and does not depend on mass.
Now consider the block sliding condition:
mg sin θ − f max = ma
mg sin θ − μmg cos θ = ma
∴ a = g(sin θ − μ cos θ)
From the above equation it is clear that acceleration does not depend on the mass but depends on θ and μ.
Question-10 :-
A boy of mass M is applying a horizontal force to slide a box of mass M’ on a rough horizontal surface. The coefficient of friction between the shoes of the boy and the floor is μ and that between the box and the floor is μ’. In which of the following cases it is certainly not possible to slide the box?
(a) μ < μ’, M < M’
(b) μ > μ’, M < M’
(c) μ < μ’, M > M’
(d) μ > μ’, M > M’
Answer-10 :-
The option (a) μ < μ’, M < M’ is correct
Explanation:
Let T be the force applied by the boy on the block.
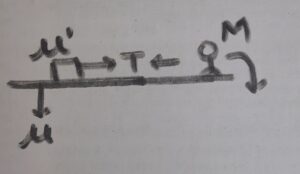
Free body diagram for the box:

The condition for preventing the slide is
fmax > T
μ’M’g > T (i)
Now see the free body diagram of a boy of mass M:

f max = μmg
The condition for preventing the slide is
f max > T
μmg > T
The condition for sliding the entire system (block and boy) is
f’ > f (block is not slide)
μ’M’g > μmg
μ’M’ > μm
μ < μ’
m < M’
—: End of Friction Obj-1 (MCQ-1) HC Verma Solutions Ch-6 Vol-I :–
Thanks




