Mensuration Class-7 RS Aggarwal ICSE Goyal Brother

Mensuration Class-7 RS Aggarwal ICSE Goyal Brother Prakashan Chapter-23 Solutions. We provide step by step Solutions of Exercise / lesson-23 Properties of Mensuration  for ICSE Class-7 RS Aggarwal Mathematics.

Our Solutions contain all type Questions with Exe-23 A, Exe-23 A, Exe-23 B, Exe-23 C, Exe-23 D, Exe-23 E, Exe-23 F, Exe-23 G and MCQs Exe-23 H, with Mental Maths to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-7 Mathematics.

Board	ICSE
Publications	Goyal brothers Prakshan
Subject	Maths
Class	7th
Chapter-23	Mensuration
Writer	RS Aggrawal
Book Name	Foundation
Topics	Solution of Exe-23 A, Exe-23 A, Exe-23 B, Exe-23 C, Exe-23 D, Exe-23 E, Exe-23 F, Exe-23 G and MCQs Exe-23 H, with Mental Maths to develop skill and confidence
Academic Session	2021-2022

Mensuration Class-7 RS Aggarwal ICSE Goyal Brother Prakashan Chapter-23 Solutions

---

-: Select Topic :-

Exe-23 A,

  Exe-23 B,

 Exe-23 C,

 Exe-23 D,

Exe-23 E,

Exe-23 F,

Exe-23 G

MCQs Exe-23 H,

  Mental Maths

---

Mensuration is the branch of Mathematics that studies the measurement of the geometric figures and their parameters like length, volume, shape, surface area, lateral surface area, etc.

Mensuration Formulas: Area Formulas & Perimeter Formulas

Before getting into the list of Mensuration formulas, i.e. area formulas and perimeter formulas of all major geometric shapes, let’s have a look at the definition of ‘area’ and ‘perimeter

What Is Area Of A Geometric Figure?

The area of a closed geometric figure is basically the size or extent of the two-dimensional surface of the figure

What Is Perimeter Of A Geometric Figure?

The perimeter of a closed geometric figure is the total length of the boundary of the figure.

 Mensuration :- Important Unit related  2D

Terms	Abbreviation	Unit	Definition
Area	A	m2 or cm2	The area is the surface which is covered by the closed shape.
Perimeter	P	cm or m	The measure of the continuous line along the boundary of the given figure is called a Perimeter.
Volume	V	cm3 or m3	The space occupied by a 3D shape is called a Volume.
Curved Surface Area	CSA	m2 or cm2	If there’s a curved surface, then the total area is called a Curved Surface area. Example: Sphere
Lateral Surface area	LSA	m2 or cm2	The total area of all the lateral surfaces that surrounds the given figure is called the Lateral Surface area.
Total Surface Area	TSA	m2 or cm2	The sum of all the curved and lateral surface areas is called the Total Surface area.
Square Unit	–	m2 or cm2	The area covered by a square of side one unit is called a Square unit.
Cube Unit	–	m3 or cm3	The volume occupied by a cube of one side one unit

Area Formulas Of Common Geometric Figures

Geometrical Shapes	Area Formulas	Variables
Area of Square	Area = a x a = a2	a = Length of each side of the square
Area of Rectangle	Area = l x b	l = Length of the rectangle b = Breadth of the rectangle
Area of Triangle	Area = (b x h)/2	b = Length of the base of the triangle h = Height of the triangle
Area of Circle	πr2	π = 22/7 = 3.14159 (approx) r = Radius of the circle
Area of Parallelogram	Area = b x h	b = Base of the parallelogram h = Height of the parallelogram
Area of Trapezium	Area = {(a + b) x h}/2	a + b= Sum of the lengths of the two parallel sides of the trapezoid, i.e. Base 1 and Base 2 h = Perpendicular distance between the two parallel sides
Area of Rhombus	Area = (p x q)/2	p = Length of 1st diagonal q = Length of second diagonal pq = Product of the two diagonals
Area of Ellipse	Area = πab	a = Major radius b = Minor radius

Perimeter Formulas Of Common Geometrical Figures

Geometrical Shapes	Perimeter Formulas	Variables
Perimeter of Square	Perimeter = 4a	a = Length of each side of the square
Perimeter of Rectangle	Perimeter = 2 (l + b)	l = Length of the rectangle b = Breadth of the rectangle
Perimeter of Triangle	Perimeter = a + b + c	a, b and c are the lengths of the three sides of the triangle
Perimeter of Circle	Perimeter = πd = 2πr	π = 22/7 = 3.14159 (approx) r = Radius of the circle d = Diameter of the circle
Perimeter of Parallelogram	Perimeter = 2 (l + b)	l = Length of the parallelogram b = Breadth of the parallelogram
Perimeter of Trapezium	Perimeter = a + b + c + d	a, b, c, d are the lengths of the four sides of the trapezoid
Perimeter of Rhombus	Perimeter = 4a	a = Length of each side of the rhombus
Perimeter of Kite	Perimeter= 2a + 2b	a = Length of each side of the first pair b = Length of each side of the second pair

Additional Area And Parameter Formulas

Some additional formulas to calculate area and perimeters are as under:

Area of a Triangle of Given Sides – a, b, c	Area = √ [s (s – a) (s – b) (s – c)]	s = Semi-perimeter of the triangle = (a + b + c)/2
Area of an Isosceles Triangle	Area = (base x height)/2 base = b height = √(a2 − b2/4)	a = Length of each of the equal sides of the isosceles triangle b = Length of the base
Perimeter of an Isosceles Triangle	Perimeter = 2a + b	a = Length of each of the equal sides of the isosceles triangle b = Length of the base
Area of an Equilateral Triangle	Area = (√3 x a2)/4	a = Length of each side of the equilateral triangle
Perimeter of an Equilateral Triangle	Perimeter = 3a	a = Length of each side of the equilateral triangle
Perimeter of a Semi-Circle	Perimeter = πr + d = 3πr	r = Radius of the circle d = 2r = Diameter of the circle
Area of a Semi-Circle	Area = (πr2) x (1/2)	r = Radius of the circle

 

---

 Exe-23 A,

Mensuration Class-7 RS Aggarwal ICSE Goyal Brother Prakashan

Page 247

Question 1:

Find the perimeters of :

(i)………….

…………….

Question 2:

………………………

…………………….

……………………..

Question 11:

The wheel of a car rotated 1000 times  in travelling a distance of 1.76 km. Find the radius of the wheel.

---

  Exe-23 B,

Mensuration Class-7 RS Aggarwal ICSE Goyal Brother Prakashan

Page 250

Question 1:

Find the area of each of the figure drawn on the unit ……………….. has side 1 cm.

Answer :

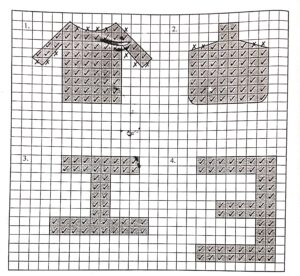
1.Shirt

(i)Place the shirt on the square grid sheet , as shown in the figure.

(ii) Draw it’s outer boundary using a sharp pencil , as shown in the figure .

(iii)Remove the shirt.

(iv)Mark(right) each one of the complete squares lying within the boundary of the shirt .

(v)Mark(right) each one of the  squares lying either half or more than half within the boundary of the shirt .

(vi) Mark(wrong) each of the squares lying less than half within the boundary of the shirt .

(vii)Count all the  squares marked (right) and neglect all the squares marked (wrong) or unmarked .

(viii)The counted squares give the area of the shirt in sq. cm.Here the area of the shirt is 60 ​\( cm^{2} \)​

2. Bottle

(i) Place the bottle on the unit square grid sheet ,as shown in the figure.

(ii)Draw its outer boundary using a sharp pencil,as shown in the figure.

(iii)Remove the bottle.

(iv)Mark (right) each one of the complete squares lying within the boundary of the bottle.

(v)Mark (right) each one of the  squares lying lying either half or more than half within the boundary of the bottle.

(vi)Mark(wrong) each of the squares lying less than half within the             boundary of the bottle .

(vii)Count all the  squares marked (right) and neglect all the squares marked (wrong) or unmarked .

(viii) The counted square give the area of the bottle in sq. cm. Here , the area of the bottle is 56 ​\( cm^{2} \)​.

3- Alphabet- 1

(i) Place the alphabet – I on the unit square  grid sheet ,as shown in the figure .

(ii) Draw it’s outer boundary using a sharp pencil , as shown in the figure .

(iii) Remove the Alphabet -I.

(iv)Mark (right) each one of the complete squares lying within the boundary of the Alphabet -I.

(v)Mark (right) each one of the  squares lying lying either half or more than half within the boundary of the Alphabet -I.

(vi))Mark(wrong) each of the squares lying less than half within the             boundary of the Alphabet -I.

(vii)Count all the  squares marked (right) and neglect all the squares marked (wrong) or unmarked .

(viii)The counted squares  give the area of the Alphabet -I.   in sq. cm. Here , the area of the Alphabet -I.    is 46  ​\( cm^{2} \)​.

4. Inverted E

(i)Place the inverted E on the unit square  grid sheet ,as shown in the figure .

(ii)Draw it’s outer boundary using a sharp pencil , as shown in the figure .

(iii)Remove the inverted E.

(iv)Mark (right) each one of the complete squares lying within the boundary of the  inverted E.

(v)Mark (right) each one of the  squares lying lying either half or more than half within the boundary of the inverted E.

(vi)Mark(wrong) each of the squares lying less than half within the             boundary of the inverted E.

(vii)Count all the  squares marked (right) and neglect all the squares marked (wrong) or unmarked .

(viii)The counted squares  give the area of the Alphabet -I.   in sq. cm. Here , the area of the  inverted E. is 56  \( cm^{2} \)​.

---

 Exe-23 C,

Mensuration Class-7 RS Aggarwal ICSE Goyal Brother Prakashan

Page 255

Question 1:

Find the perimeter and area of a rectangle having :

(i)……………….

…………………..

Question 2:

……………………..

……………………..

………………………

Question 12:

Find the area and perimeter of the …………….. following figures

…………….

---

 Exe-23 D,

Mensuration Class-7 RS Aggarwal ICSE Goyal Brother Prakashan

Page 258

Question 1:

A room is 10 m long …………….. 236 per m².

Question 2:

………………………

………………………

………………………

Question 8:

Find the area of the shaded region in each of the following figure :

---

Exe-23 E,

Mensuration Class-7 RS Aggarwal ICSE Goyal Brother Prakashan

Page 261-262

Question 1:

Find the area of the triangle, having :

‘(i)…………

…………………

Question 2:

……………………..

………………………

………………………

Question 18:

Find the area ………………….. DA = 48 cm.

---

Exe-23 F,

Mensuration Class-7 RS Aggarwal ICSE Goyal Brother Prakashan

Page 265-266

Question 1:

Find the area of the parallelogram having :

(i)………………

…………………..

Question 2:

…………………….

./……………………

……………………….

Question 11:

Find the area of the shaded region of each of the figure :

---

Exe-23 G

Mensuration Class-7 RS Aggarwal ICSE Goyal Brother Prakashan

Page 268

Question 1:

Find the area of a circle whose radius is :

(i) 2.8 m

(ii) 8.4 m

Question 2:

…………………….

……………………..

……………………….

Question 14:

The area of a circle garden ……………………… 2002 m² find :

(i)………………..

………………..

---

MCQs Exe-23 H,

Mensuration Class-7 RS Aggarwal ICSE Goyal Brother Prakashan

Page 268-269

Choose the correct option in each of the following

Question 1:

The length of the diagonal ……………… b unit is .

…………………..

Question 2:

………………………

……………………….

………………………

Question 15:

The area of a ……………. is equal to

………………….

---

  Mental Maths

Mensuration Class-7 RS Aggarwal ICSE Goyal Brother Prakashan

Page 269

1. Fill in the blanks :

(i)The perimeter of a simple closed figure is the length of it’s Boundary.

(ii)The Perimeter of a circle is called it’s circumference.

(iii)Pie (π ) is the ratio of the circumference of any circle to it’s diameter.

(iv)The area of a simple closed figure is the measure of the surface enclosed by it

(v)An area of 1 hectare is equal to 10000​\( m^{2} \)​.

(vi) A unit square grid sheet is a sheet containing horizontal and vertical lines forming squares , each of dimensions 1 cm*1 cm.

(vii) In a triangle having lengths a units , b units and c units respectively , if s=​\( \frac{a+b+c}{2} \)​units, then s is called the semi perimeter of the triangle.

(viii)The area of a Triangle ABC having BE ⊥ AC,is ​\( \frac{1}{2}AC*BE sq.units \)​.

(ix)Area of a right triangle is equal to ​\( \frac{1}{2} \)​Base *Height.

(x)Area of a  triangle having sides of lengths a units , b units and c units respectively and semiperimeter s unit is  ​\( \sqrt{s(s-a)(s-b)(s-c)} \)​sq.units.

(x) The area of a parallelogram is equal to the product of the length of side and the corresponding height.

(xi) Area of a rhombus is equal to ​\( \frac{1}{2} \)​* Product of diagonals.

(xii)The Region enclosed between two concentric circles of different radii is called a ring.

 

---

Frequently Asked Questions