Newton Law of Motion Exercise Questions Solutions HC Verma Ch-5 Concept of Physics Vol-1 for ISC Class-11. Step by Step Solution of Exercise Questions of Ch-5 Newton Law of Motion HC Verma Concept of Physics . Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
Newton Law of Motion Exercise Questions Solutions HC Verma Ch-5 Concept of Physics Vol-1 for ISC Class-11
| Board | ISC and other board |
| Publications | Bharti Bhawan Publishers |
| Ch-5 | Newton Law of Motion |
| Class | 11 |
| Vol | 1st |
| writer | H C Verma |
| Book Name | Concept of Physics |
| Topics | Solution of Exercise Questions |
| Page-Number | 79, 80, 81, 82, 83 |
-: Select Topics :-
Exercise (Currently Open)
Newton Law of Motion Exercise Questions Solutions
(HC Verma Ch-5 Concept of Physics Vol-1 for ISC Class-11)
Page-79
Question-1
A block of mass 2 kg placed on a long frictionless horizontal table is pulled horizontally by a constant force F. It is found to move 10 m in the first seconds. Find the magnitude of F.
Answer-1
Mass of the block, m = 2 kg,
Distance covered, S = 10 m and initial velocity, u = 0
Let a be the acceleration of the block.
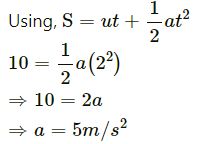
∴ Force, F = ma = 2 × 5 = 10 N
Question-2
car moving at 40 km/hr is to be stopped by applying brakes in the next 4 m. If the car weighs 2000 kg, what average force must be applied to stop it?
Answer-2
Initial speed of the car, u = 40 km/hr
= 4000 / 3600
=11.11 m/s
Final speed of the car, v = 0
Mass of the car, m = 2000 kg
Distance to be travelled by the car before coming to rest, s = 4m
Acceleration,

∴ Average force to be applied to stop the car, F = ma
⇒ F = 2000 × 15.42 ≈ 3.1 × 104 N
Question-3
In a TV picture tube, electrons are ejected from the cathode with negligible speed and they attain a velocity of 5 × 106 m/s in travelling one centimetre. Assuming straight-line motion, find the constant force exerted on the electrons. The mass of an electron is 9.1 × 10−31 kg.
Answer-3
Initial velocity of the electrons is negligible, i.e. u = 0.
Final velocity of the electrons, v = 5 × 106 m/s
Distance travelled by the electrons,
s = 1 cm = 1 × 10−2 m
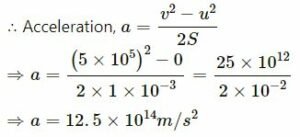
So, force on the electrons, F = ma
⇒ F = 9.1 × 10−31 × 12.5 × 10−14
= 1.1 × 10−15 N
Question-4
A block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block by another string. Find the tensions in the two strings. Take g = 10 m/s2.
Answer-4
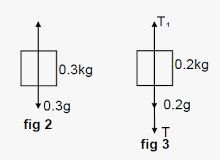
From the free-body diagram of the 0.3 kg block,
T = 0.3g
⇒ T= 0.3 × 10 = 3 N
Now, from the free-body diagram of the 0.2 kg block,
T1 = 0.2g + T
⇒ T1= 0.2 × 10 + 3 = 5 N
∴ The tensions in the two strings are 5 N and 3 N, respectively.
Question-5
Two blocks of equal mass m are tied to each other through a light string. One of the blocks is pulled along the line joining them with a constant force F. Find the tension in the string joining the blocks.
Answer-5
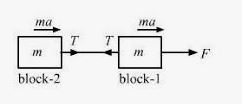
Let a be the common acceleration of the blocks.
For block 1,
F−T = m a ….(i)
For block 2,
T = m a …(ii)
Subtracting equation (ii) from (i), we get:
F−2T=0
⇒T=F / 2
Question-6
A particle of mass 50 g moves in a straight line. The variation of speed with time is shown in figure ( 5-E.1). Find the force acting on the particle at t = 2, 4 and 6 seconds.
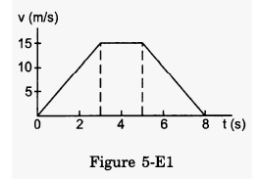
Answer-6
Mass of the particle, m = 50 g = 5 × 10−2 kg
Slope of the v-t graph gives acceleration.
At t = 2 s,
Slope = 15 / 3
= 5 m /s2
So, acceleration, a = 5 m/s2
F = ma = 5 × 10−2 × 5
⇒ F = 0.25 N along the motion.
At t = 4 s,
Slope = 0
So, acceleration, a = 0
⇒ F = 0
At t = 6 sec,
Slope =−15 / 3
=−5m/s2
So, acceleration, a = − 5 m/s2
F = ma
= − 5 × 10−2 × 5
⇒ F = − 0.25 N along the motion
or, F = 0.25 N opposite the motion
Question-7
Two blocks A and B of mass mA and mB , respectively, are kept in contact on a frictionless table. The experimenter pushes block A from behind, so that the blocks accelerate. If block A exerts force F on block B, what is the force exerted by the experimenter on block A?
Question-7
Let F’ = force exerted by the experimenter on block A and F be the force exerted by block A on block B.

Let a be the acceleration produced in the system.
For block A,
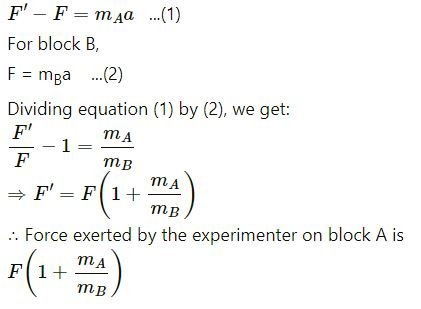
Question-8
Raindrops of radius 1 mm and mass 4 mg are falling with a speed of 30 m/s on the head of a bald person. The drops splash on the head and come to rest. Assuming equivalently that the drops cover a distance equal to their radii on the head, estimate the force exerted by each drop on the head.
Answer-8
Radius of a raindrop, r = 1 mm = 10−3 m
Mass of a raindrop, m = 4 mg = 4 × 10−6 kg
Distance coved by the drop on the head, s = 10−3 m
Initial speed of the drop, v = 0
Final speed of the drop, u = 30 m/s

Force, F = ma
⇒ F = 4 × 10−6 × 4.5 × 105 = 1.8 N
Question-9
A particle of mass 0.3 kg is subjected to a force F = −kx with k = 15 N/m. What will be its initial acceleration if it is released from a point x = 20 cm?
Answer-9
Displacement of the particle from the mean position, x = 20 cm = 0.2 m
k = 15 N/m
Mass of the particle, m = 0.3 kg
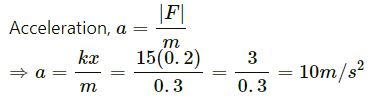
So, the initial acceleration when the particle is released from a point x = 20 cm is 10 m/s2.
Question-10
Both the springs shown in figure ( 5-E.2) the following figure are unstretched. If the block is displaced by a distance x and released, what will be the initial acceleration?

Answer-10
Let the block m be displaced towards left by displacement x.
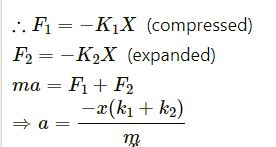
![]()
opposite the displacement or towards the mean position
Question-11
A small block B is placed on another block A of mass 5 kg and length 20 cm. Initially, the block B is near the right end of block A (Figure 5-E.3). A constant horizontal force of 10 N is applied to the block A. All the surfaces are assumed frictionless. Find the time that elapses before block B separates from A.
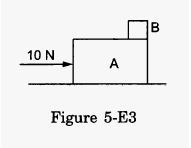
Answer-11
Mass of block A, m = 5 kg
F = m a = 10 N
⇒a = 10 / 5
= 2m/s2
As there is no friction between A and B, when block A moves, block B remains at rest in its position.
Initial velocity of A, u = 0
Distance covered by A to separate out,
s = 0.2 m
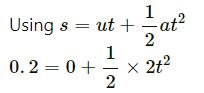
⇒ t2 = 0.2
⇒ t = 0.44 s ≈ 0.45 s
Question-12
A man has fallen into a ditch of width d and two of his friends are slowly pulling him out using a light rope and two fixed pulleys as shown in Figure (5-E.4). Show that the force (assumed equal for both the friends) exerted by each friend on the road increases as the man moves up. Find the force when the man is at a depth h.
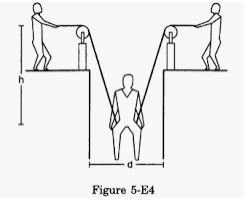
Answer-12
(a) At any depth, let the ropes makes an angle θ with the vertical.
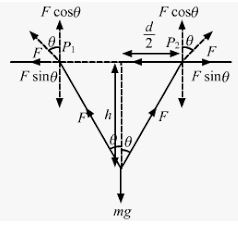
From the free-body diagram,
Fcosθ + Fcosθ − mg = 0
2Fcosθ = mg
⇒ F =mg / 2cosθ
As the man moves up, θ increases, i.e. cosθ decreases. Thus, F increases.
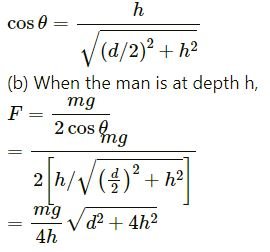
page-80
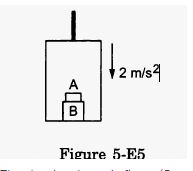
Question-13
The elevator shown in figure (5-E.5) is descending with an acceleration of 2 m/s2. The mass of the block A is 0.5 kg. What force is exerted by the block A on the block B?
Answer-13
When the elevator is descending, a pseudo-force acts on it in the upward direction, as shown in the figure.

From the free-body diagram of block A,
mg−N = ma
N = m (g−a)
⇒N = 0.5 (10−2)
=4N
So, the force exerted by the block A on the block B is 4 N..
Question-14
A pendulum bob of mass 50 g is suspended from the ceiling of an elevator. Find the tension in the string if the elevator (a) goes up with acceleration 1.2 m/s2, (b) goes up with deceleration 1.2 m/s2, (c) goes up with uniform velocity, (d) goes down with acceleration 1.2 m/s2, (e) goes down with deceleration 1.2 m/s2 and (f) goes down with uniform velocity.
Answer-14
(a) When the elevator goes up with acceleration 1.2 m/s2:
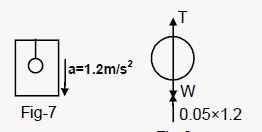
T= mg+ma
⇒ T = 0.05 (9.8 + 1.2) = 0.55 N
(b) Goes up with deceleration 1.2 m/s2 :

T=mg+m(−a)=m(g−a)
⇒ T = 0.05 (9.8 − 1.2) = 0.43 N
(c) Goes up with uniform velocity:
T=mg
⇒ T = 0.05 × 9.8 = 0.49 N
(d) Goes down with acceleration 1.2 m/s2 :
T+ma=mg
⇒T=m(g−a)
⇒ T = 0.05 (9.8 − 1.2) = 0.43 N
(e) Goes down with deceleration 1.2 m/s2 :
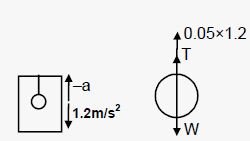
T+m(−a)=mg
⇒T=m(g+a)
⇒ T = 0.05 (9.8 + 1.2) = 0.55 N
(f) Goes down with uniform velocity:

T=mg
⇒ T = 0.05 × 9.8 = 0.49 N
Question-15
A person is standing on a weighing machine placed on the floor of an elevator. The elevator starts going up with some acceleration, moves with uniform velocity for a while and finally decelerates to stop. The maximum and the minimum weights recorded are 72 kg and 60 kg, respectively. Assuming that the magnitudes of acceleration and deceleration are the same, find (a) the true weight of the person and (b) the magnitude of the acceleration. Take g = 9.9 m/s2.
Answer-15
(a)
Maximum weight will be recorded when the elevator accelerates upwards.
Let N be the normal reaction on the person by the weighing machine.
So, from the free-body diagram of the person,
N=mg+ma …(1)
This is maximum weight, N = 72 × 9.9 N
When decelerating upwards, minimum weight will be recorded.
N′=mg+m(−a) …(2)
This is minimum weight, N’ = 60 × 9.9 N
From equations (1) and (2), we have:
2 mg = 1306.8
⇒m=1306.8 / 2×9.9
=66 kg
So, the true mass of the man is 66 kg.
And true weight = 66 × 9.9 = 653.4 N
(b)
Using equation (1) to find the acceleration, we get:
mg + ma = 72 × 9.9
Question-16
Find the reading of the spring balance shown in figure (5- E.6). The elevator is going up with an acceleration g/10, the pulley and the string are light and the pulley is smooth.
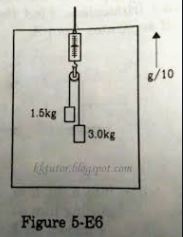
Answer-16
Let the left and right blocks be A and B, respectively.
And let the acceleration of the 3 kg mass relative to the elevator be ‘a‘ in the downward direction.


Question-17
A block of 2 kg is suspended from a ceiling by a massless spring of spring constant k = 100 N/m. What is the elongation of the spring? If another 1 kg is added to the block, what would be the further elongation?
Answer-17
mass of the first block, m = 2 kg
k = 100 N/m
Let elongation in the spring be x.
From the free-body diagram,
kx = mg

Question-18
Suppose the ceiling in the previous problem is that of an elevator which is going up with an acceleration of 2.0 m/s2. Find the elongation.
Answer-18
When the ceiling of the elevator is going up with an acceleration ‘a’, then a pseudo-force acts on the block in the downward direction.
a = 2 m/s2
From the free-body diagram of the block,
kx = mg + ma
⇒ kx = 2g + 2a
= 2 × 9.8 + 2 × 2
= 19.6 + 4
⇒x =23.6 / 100
=0.236≈0.24 m
When 1 kg body is added,
total mass = (2 + 1) kg = 3 kg
Let elongation be x’.
∴ kx’ = 3g + 3a = 3 × 9.8 + 6
=0.354≈0.36m
So, further elongation
= 0.36 − 0.24 = 0.12 m.
Question-19
Answer-19
Let M be mass of the balloon.
Let the air resistance force on balloon be F .
Given that F ∝ v.
⇒ F = kv,
where k = proportionality constant.
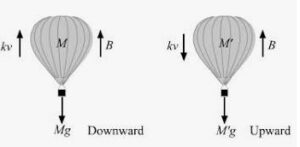
When the balloon is moving downward with constant velocity,
B + kv = Mg …(i)
⇒M =( B + kv ) / g
Let the mass of the balloon be M’ so that it can rise with a constant velocity v in the upward direction.
B = Mg + kv

Question-20
An empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the rate of g/6?
Answer-20
Let U be the upward force of water acting on the plastic box.
Let m be the initial mass of the plastic box.
When the empty plastic box is accelerating upward,
U−mg = mg / 6
⇒U = 7mg / 6
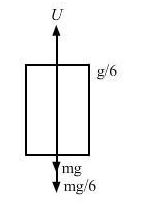
⇒m = 6U / 7g….(i)
Let M be the final mass of the box after putting some sand in it.

Question-21
A force ![]() is exerted on a particle in addition to the force of gravity, where v is the velocity of the particle and
is exerted on a particle in addition to the force of gravity, where v is the velocity of the particle and ![]() is a constant vector in the horizontal direction. With what minimum speed, a particle of mass m be projected so that it continues to move un deflected with a constant velocity?
is a constant vector in the horizontal direction. With what minimum speed, a particle of mass m be projected so that it continues to move un deflected with a constant velocity?
Answer-21
For the particle to move without being deflected and with constant velocity, the net force on the particle should be zero.

Question-22
In a simple Atwood machine, two unequal masses m1 and m2 are connected by a string going over a clamped light smooth pulley. In a typical arrangement (figure 5 -E.7), m1 = 300 g and m2 = 600 g. The system is released from rest. (a) Find the distance travelled by the first block in the first two seconds; (b) find the tension in the string; (c) find the force exerted by the clamp on the pulley.

Answer-22
The masses of the blocks are m1 = 0.3 kg and m2 = 0.6 kg
For mass m1,
T − m1g = m1a …(i)
For mass m2,
m2g − T= m2a …(ii)
Adding equations (i) and (ii), we get:
g(m2 − m1) = a(m1 + m2)

(b) From equation (i),
T = m1 (g + a)
= 0.3 (3.8 + 3.26) = 3.9 N
(c) The force exerted by the clamp on the pulley,
F = 2T = 2 × 3.9 = 7.8 N
Question-23
Consider the Atwood machine of the previous problem. The larger mass is stopped for a moment, 2.0 s after the system is set into motion. Find the time that elapses before the string is tight again.
Answer-23
a = 3.26 m/s2, T = 3.9 N
After 2 s, velocity of mass m1,
v = u + at = 0 + 3.26 × 2
= 6.52 m/s upward
At this time, m2 is moving 6.52 m/s downward.
At time 2 s, m2 stops for a moment. But m1 is moving upward with velocity 6.52 m/s. It will continue to move till final velocity (at highest point) becomes zero.
Here, v = 0, u = 6.52 m/s
a = −g = − 9.8 m/s2
v = u + at = 6.52 + (−9.8)t
⇒t = 6.52 / 9.8
= 2 / 3 sec
After this time, the mass m1 also starts moving downward.
So, the string becomes tight again after 2 / 3 sec
Question-24
Figure ( 5 -E.8) shows a uniform rod of length 30 cm and mass 3.0 kg. The strings shown in the figure are pulled by constant forces of 20 N and 32 N. Find the force exerted by the 20 cm part of the rod on the 10 cm part. All the surfaces are smooth and the strings and the pulleys are light.
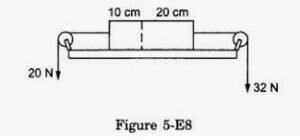
Answer-24
Mass per unit length =3 / 30kg/cm
= 0.10 kg/cm
Mass of the 10 cm part, m1 = 1 kg
Mass of the 20 cm part, m2 = 2 kg
Let F = contact force between them.
From the free-body diagram,

So, contact force,
F = 20 + 1a
F = 20 + 4
= 24 N
Page-81
Question-25
Consider the situation shown in figure ( 5 -E.9) All the surfaces are frictionless and the string and the pulley are light. Find the magnitude of acceleration of the two blocks

Answer-25
Mass of each block is 1 kg,

Question-26
A constant force F = m2g/2 is applied on the block of mass m1 as shown in figure ( 5 -E.10) . The string and the pulley are light and the surface of the table is smooth. Find the acceleration of m1.
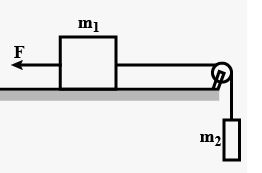
Answer-26
block of mass m1,
m1a = T − F …(i)
block of mass m2,
m2a = m2g − T …(ii)
Adding .(i) and.(ii) equations

Question-27
In figure ( 5 -E.11), m1 = 5 kg, m2 = 2 kg and F = 1 N. Find the acceleration of either block. Describe the motion of m1 if the string breaks but F continues to act.

figure ( 5 -E.11)
Answer-27
Let the acceleration of the blocks be a.
m1a = m1g + F − T …(i)
m2a = T − m2g − F …(ii)
Adding .(i) and.(ii) equations

Hence, acceleration of the block is 4.2 m/s2.
After the string breaks, m1 moves downward with force F acting downward. Then,
m1a = F + m1g
5a = 1 + 5g
⇒a= (5g+1 ) / 5
= g + 0.2m /s²
Question-28
Let m1 = 1 kg, m2 = 2 kg and m3 = 3 kg in figure ( 5 -E.12). Find the accelerations of m1, m2 and m3. The string from the upper pulley to m1 is 20 cm when the system is released from rest. How long will it take before m1 strikes the pulley?

Answer-28
Suppose the block m1 moves upward with acceleration a1 and the blocks m2 and m3have relative acceleration a2 due to the difference of weight between them.
So, the actual acceleration of the blocks m1, m2 and m3 will be a1, (a1 − a2) and (a1 + a2), as shown.
T − 1g − 1a1 = 0 …(i)

From equations (i) and (ii), eliminating T
1g + 1a2 = 4g + 4 (a1 + a2)
5a2 − 4a1 = 3g …(iv)
From equations (ii) and (iii), we get:
2g + 2(a1 − a2) = 3g − 3 (a1 − a2)
5a1 + a2 = g …(v)
on Solving equations (iv) and (v),
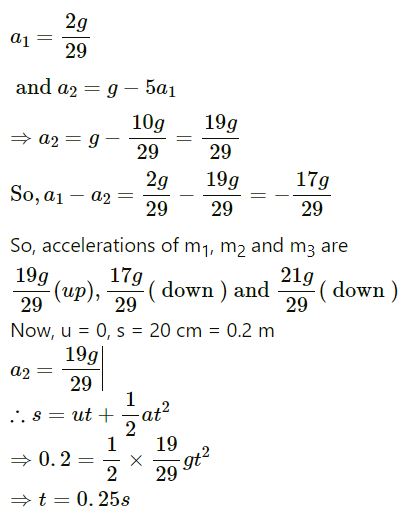
Question-29
In the previous problem, suppose m2 = 2.0 kg and m3 = 3.0 kg. What should be the mass m, so that it remains at rest?
Answer-29
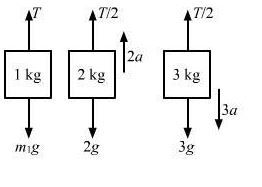
For m1 to be at rest, a1 = 0.
T − m1g = 0
T = m1g …(i)
For mass m2,
T/2 − 2g = 2a
T = 4a + 4g …(ii)
For mass m3,
3g – T/2= 2a
T = 6g − 6a …(ii)
From equations (ii) and (iii), we get:
3T – 12g = 12g – 2T
T = 24g/5= 4.08g
Putting the value of T in equation (i), we get:
m1 = 4.8kg
Question-30
Calculate the tension in the string shown in figure (5-E.13). The pulley and the string are light and all the surfaces are frictionless. Take g = 10 m/s2.
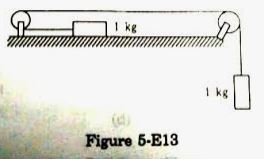
Answer-30
T + ma =mg …(i)
and T = ma …(ii)
From equations (i) and (ii), we get:
ma + ma = mg
⇒ 2ma = g
⇒a = g / 2
= 10 / 5
= 5m / s²
From equation (ii),
T = ma = 5 N
Question-31
Consider the situation shown in figure (5-E.14). Both the pulleys and the string are light and all the surfaces are frictionless. (a) Find the acceleration of the mass M; (b) find the tension in the string; (c) calculate the force exerted by the clamp on the pulley A in the figure.
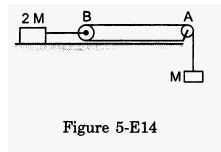
Answer-31
Let the acceleration of mass M be a.
So, the acceleration of mass 2M will be a / 2
(a) 2M (a/2) − 2T = 0
⇒ Ma = 2T
T + Ma − Mg = 0

So, the force exerted by the clamp on the pulley is √2Mg / 3 at an angle of 45° with the horizontal
Question-32
Find the acceleration of the block of mass M in the situation shown in figure (5-E.15). All the surfaces are frictionless and the pulleys and the string are light.

Answer-32
Let acceleration of the block of mass 2M be a.
So, acceleration of the block of mass M will be 2a.
M(2a) + Mgsinθ − T = 0
⇒ T = 2Ma + Mgsinθ …(i)
2T + 2Ma − 2Mg = 0
From equation (i),
2(2Ma + Mgsinθ) + 2Ma − 2Mg = 0
4Ma + 2Mgsinθ + 2Ma − Mg = 0
6Ma + 2Mgsin30° + 2Mg = 0
6Ma = Mg
⇒a= g / 6
Hence, the acceleration of mass
M = 2 a
M=2× (g / 6)
= g / 3 ( up the plane ).
Page-82
Question-33
Find the mass M of the hanging block in figure (5-E.16) that will prevent the smaller block from slipping over the triangular block. All the surfaces are frictionless and the strings and the pulleys are light.

Answer-33
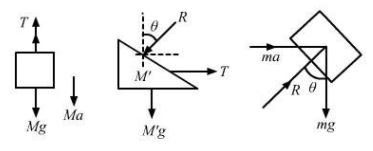
Block ‘m’ will have the same acceleration as that of M’, as it does not slip over M’.
T + Ma – Mg = 0 …(i)
T – M’a – Rsinθ = 0 …(ii)
Rsinθ – ma = 0
Rcosθ – mg = 0
Eliminating T, R and a from the above equations, we get
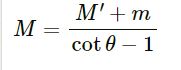
Question-34
Find the acceleration of the blocks A and B in the three situations shown in figure (5-E.17).

Answer-34
(a) 5a + T − 5g = 0
T = 5g − 5a …..(i)
Again,
(1/2) T−4g−8a = 0
⇒ T − 8g − 16a = 0
T = 8g + 16a ……(ii)
From equations (i) and (ii), we get:
5g − 5a = 8g + 16a
⇒21a =−3g−a = −9 / 7
So, the acceleration of the 5 kg mass is 97m/s²( upward ) and that of the 4 kg mass is
2a = 2g / 7 ( downward )
4a− (T / 2) = 0
⇒ 8a − T = 0
⇒ T = 8a
Again, T + 5a − 5g = 0
8a + 5a − 5g = 0
⇒ 13a − 5g = 0
⇒a= 5g / 13( downward )
Acceleration of mass 2 kg is 2a
= 10 / 13 (g) and 5 kg is = 5g / 13.
(c) T + 1a − 1g = 0
T = 1g − 1a …..(i)
Again,
T2−2g−4a=0
⇒ T − 4g − 8a = 0 …..(ii)
From equation (i)
1g − 1a − 4g − 8a = 0
⇒a = g / 3 (downward )
Acceleration of mass 1 kg is g / 3 ( upward )
Acceleration of mass 2 kg is 2g / 3 ( downward )
Question-35
Find the acceleration of the 500 g block in figure (5-E.18).

Answer-35

Given,
m1 = 100 g = 0.1 kg
m2 = 500 g = 0.5 kg
m3 = 50 g = 0.05 kg
From the figure 500 g block,
T + 0.5a − 0.5g = 0 …..(i)
From the figure 50 g block,
T1 + 0.05g − 0.05a = a ….(ii)
From the figure 100 g block,
T1 + 0.1a − T + 0.5g = 0 ….(iii)
From equation (ii),
T1 = 0.05g + 0.05a …..(iv)
From equation (i),
T1 = 0.5g − 0.5a …..(v)
Equation (iii) becomes
T1 + 0.1a − T + 0.05g = 0
From equations (iv) and (v), we get:
0.05g + 0.05a + 0.1a − 0.5g + 0.5a + 0.05g = 0
0.65a = 0.4 g

Question-36
A monkey of mass 15 kg is climbing a rope fixed to a ceiling. If it wishes to go up with an acceleration of 1 m/s2, how much force should it apply on the rope? If the rope is 5 m long and the monkey starts from rest, how much time will it take to reach the ceiling?
Answer-36
Mass of the monkey, m = 15 kg,
Acceleration of the monkey in the upward direction, a = 1 m/s2
The free-body diagram of the monkey is shown below:
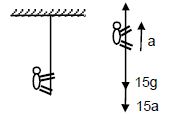
From the free-body diagram,
T − [15g + 15(a)] = 0
T − [15g + 15(1)] = 0
⇒ T = 5 (10 + 1)
⇒ T = 15 × 11 = 165 N
The monkey should apply a force of 165 N to the rope.
Initial velocity, u = 0
s = 5 m
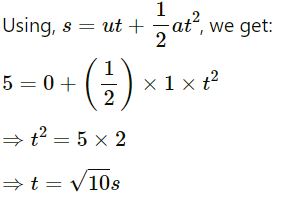
Hence, the time required to reach the ceiling is √10 s
Question-37
A monkey is climbing on a rope that goes over a smooth light pulley and supports a block of equal mass at the other end figure (5-E.19). Show that whatever force the monkey exerts on the rope, the monkey and the block move in the same direction with equal acceleration. If initially both were at rest, their separation will not change as time passes.
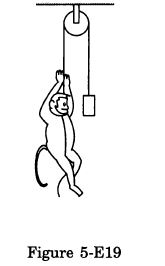
Answer-37
Suppose the monkey accelerates upward with acceleration a and the block accelerates downward with acceleration a’.
Let force exerted by the monkey be F.
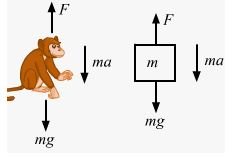
From the diagram of the monkey, we get:
F− mg − ma = 0 …(i)
⇒ F = mg + ma
Again, from the diagram of the block,
F + ma’ − mg = 0
mg + ma + ma’ − mg = 0 [From (i)]
⇒ ma = −ma’
⇒ a = −a’
If acceleration −a’ is in downward direction then the acceleration a’ will be in upward direction.
This implies that the block and the monkey move in the same direction with equal acceleration.
If initially they were at rest (no force is exerted by the monkey), then their separation will not change as time passes because both are moving same direction with equal acceleration.
Question-38
The monkey B, shown in figure (5-E.20), is holding on to the tail of monkey A that is climbing up a rope. The masses of monkeys A and B are 5 kg and 2 kg, respectively. If A can tolerate a tension of 30 N in its tail, what force should it apply on the rope in order to carry monkey B with it? Take g = 10 m/s2.
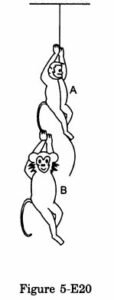
Answer-38
Let the acceleration of monkey A upwards be a, so that a maximum tension of 30 N is produced in its tail.
T − 5g − 30 − 5a = 0 …(i)
30 − 2g − 2a = 0 …(ii)
From equations (i) and (ii), we have:
T = 105 N (max.)
and a = 5 m/s2
So, A can apply a maximum force of 105 N on the rope to carry monkey B with it.
For minimum force, there is no acceleration of A and B.
T1 = weight of monkey B
⇒ T1 = 20 N
Rewriting equation (i) for monkey A, we get:
T − 5g − 20 = 0
⇒ T = 70 N
∴ To carry monkey B with it, monkey A should apply a force of magnitude between 70 N and 105 N.
Question-39
figure (5-E.21) shows a man of mass 60 kg standing on a light weighing machine kept in a box of mass 30 kg. The box is hanging from a pulley fixed to the ceiling by a light rope, the other end of which is held by the man himself. If the man manages to keep the box at rest, what is the weight recorded on the machine? What force should he exert on the rope to record his correct weight on the machine?

Question-39
(i) Given, mass of the man = 60 kg
Let W’ = apparent weight of the man in this case
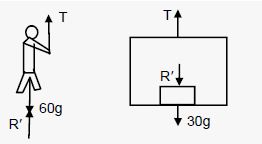
From the diagram of the man,
W’ + T − 60g = 0
⇒ T = 60g − W’ …(i)
From the diagram of the box,
T − W’ = 30g = 0 …(ii)
From equation (i), we get:
60g − W’ − W’ − 30g = 0
⇒ W’ = 15g
Hence, the weight recorded on the machine is 15 kg.
(ii) To find his actual weight, suppose the force applied by the men on the rope is T because of which the box accelerates upward with an acceleration a’.Here we need to find T′
Correct weight = W = 60g
From the diagram of the man,
T’ + W − 60g − 60a = 0
⇒ T’ − 60a = 0
⇒ T’ = 60a …(i)
From the diagram of the box,
T’ − W − 30g − 30a = 0
⇒ T’ − 60g − 30g − 30a = 0
⇒ T’ = 30a − 900 …(ii)
From equations (i) and (ii), we get:
T’ = 2T’ − 1800
T’ = 1800 N
So, the man should exert a force of 1800 N on the rope to record his correct weight on the machine.
Page-83
Question-40
A block A can slide on a frictionless incline of angle θ and length l, kept inside an elevator going up with uniform velocity v ( figure 5-E.22). Find the time taken by the block to slide down the length of the incline if it is released from the top of the incline.
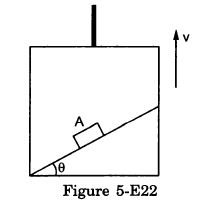
Answer-40
The force on the block which makes the body move down the plane is the component of its weight parallel to the inclined surface.
F = mg sinθ
Acceleration, g = sin θ
Initial velocity of block, u = 0
Distance to be covered
s = l
a = g sin θ
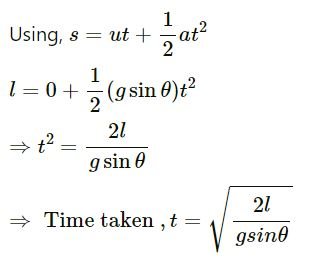
Question-41
A car is speeding up a horizontal road with acceleration a. Consider the following situations in the car: (i) A ball suspended from the ceiling by a string is maintaining a constant angle with the vertical. Find this angle. (ii) A block is kept on a smooth incline and does not slip on the incline. Find the angle of the incline with the horizontal.
Answer-41
Let the pendulum (formed by the ball and the string) make angle θ with the vertical.

From the diagram,
Tcosθ − mg = 0
Tcosθ = mg

(ii) Let the angle of the incline be θ.
From the diagram,

Question-42
A block is kept on the floor of an elevator at rest. The elevator starts descending with an acceleration of 12 m/s2. Find the displacement of the block during the first 0.2 s after the start. Take g = 10 m/s2.
Answer-42
The two bodies are separated because the elevator is moving downward with an acceleration of 12 m/s2 (>g) and the body moves with acceleration, g = 10 m/s2 [Freely falling body]
Now, for the block:
g = 10 m/s2, u = 0, t = 0.2 s
So, the distance travelled by the block is given by
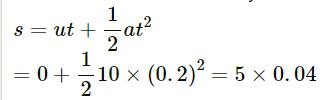
= 0 . 2 m = 20 cm
The displacement of the body is 20 cm during the first 0.2 s.
—: End of Newton Law of Motion Exercise Solutions Concept of Physics:–
Thanks


