ML Aggarwal Trigonometrical Ratios of Standards Angles Exe-18.1 Class 9 ICSE Maths APC Understanding Solutions. Solutions of Exe-18.1. This post is the Solutions of ML Aggarwal Chapter 18 – Trigonometrical Ratios of Standards Angles for ICSE Maths Class-9. APC Understanding ML Aggarwal Solutions (APC) Avichal Publication Solutions of Chapter-18 Trigonometrical Ratios of Standards Angles for ICSE Board Class-9. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Trigonometrical Ratios Exe-18.1 Class 9 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 9th |
| Chapter-18 | Trigonometrical Ratios of Standards Angles |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-18.1 Questions |
| Edition | 2021-2022 |
Exe-18.1 Solutions of ML Aggarwal for ICSE Class-9 Ch-18, Trigonometrical Ratios of Standards Angles
Note:- Before viewing Solutions of Chapter -18 Trigonometrical Ratios of Standards Angles Class-9 of ML Aggarwal Solutions . Read the Chapter Carefully. Then solve all example given in Exercise-18.1, Exercise-18.2, MCQs, Chapter Test.
Trigonometrical Ratios of Standards Angles Exercise-18.1
ML Aggarwal Class 9 ICSE Maths Solutions
Page 428
Question 1. Find the values of
(i) 7 sin 30° cos 60°
(ii) 3 sin2 45° + 2 cos2 60°
(iii) cos2 45° + sin2 60° + sin2 30°
(iv) cos 90° + cos2 45° sin 30° tan 45°.
Answer :
(i) 7 sin 30° cos 60°
= 7 ×½ ×½
= (7×1×1)/(2×2)
= 7/4
(ii) 3 sin2 45° + 2 cos2 60°
= 3×(1/√2)2 + [2×(1/2)2]
= (3×½) + (2 × ¼)
= 3/2 + ½
= (3 + 1)/2
= 4/2
= 2
(iii) cos2 45° + sin2 60° + sin2 30°
= (1/√2)2 + (√3/2)2 + (1/2)2
= ½ + ¾ + ¼
= (2 + 3 + 1)/4
= 6/4
= 3/2
(iv) cos 90° + cos2 45° sin 30° tan 45°
= 0 + (1/√2)2 × ½ × 1
= ½ × ½ × 1
= ¼
Question 2. Find the values of
(i) (sin245° + cos245°)/tan260°
(ii) (sin30° – sin90° + 2cos0°)/tan2 60°
(iii) 4/3 tan230° + sin260° – 3cos260° + 3/4 tan260° – 2tan245°
Answer :
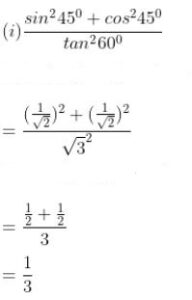
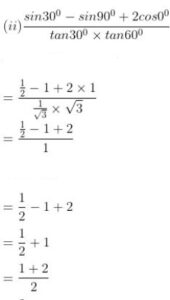
(iii) 4/3 tan230° + sin260° – 3cos260° + ¾tan260° – 2tan245°
= 4/3(1/√3)2 + (√3/2)2 – 3(1/2)2 + ¾×(√3)2 – 2×12
= (4/3× 1/3) + ¾ – (3 × ¼) + (¾ ×3) – (2×1)
= 4/9 + ¾ – 3/4 + 9/4 – 2
= 4/9 + 9/4 – 2
Taking LCM
= (16 + 81 – 72)/36
= (97 – 72)/36
= 25/36
Question 3. Find the values of
(i) (sin30°/cos245°) – 3tan30° + 5cos90°
(ii) 2√2 cos45° cos60° + 2√3 sin30° tan60° – cos30°
(iii) 4/5 tan260° – (2/sin230°) – 3/4 tan230°
Answer :
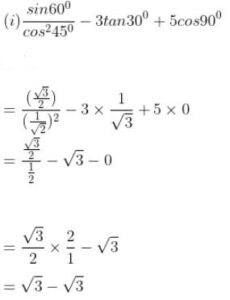
= 0
(ii) 2√2 cos 45° cos 60° + 2√3 sin 30° tan 60° – cos 0°
= 2√2 × 1/√2 × ½ + 2√3 × ½ × √3 – 1
= 2 × 1/1 × 1/2 + 2 × 3 × ½ – 1
= 1 + 3 – 1
= 3
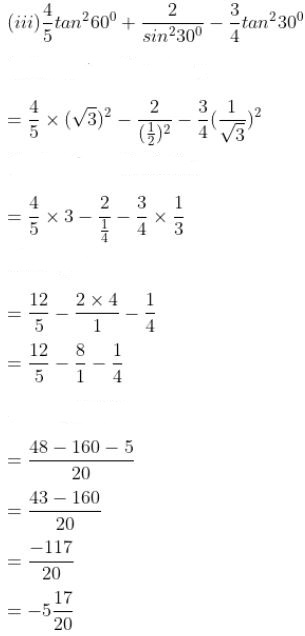
Trigonometrical Ratios of Standards Angles Exercise-18.1
ML Aggarwal Class 9 ICSE Maths Solutions
Page 429
Question 4. Prove That.
(i) cos2 30° + sin 30° + tan2 45° = 2 ¼
(ii) 4 (sin4 30° + cos4 60°) – 3 (cos2 45° – sin2 90°) = 2
(iii) cos 60° = cos2 30° – sin2 30°.
Answer :
(i) cos2 30° + sin 30° + tan2 45° = 2 ¼
LHS = cos2 30° + sin 30° + tan2 45°
= (√3/2)2 + ½ + 12
= ¾ + ½ + 1
= (3 + 2 + 4)/4
= 9/4
= 2 ¼
= RHS
Hence, LHS = RHS.
(ii) 4 (sin4 30° + cos4 60°) – 3 (cos2 45° – sin2 90°) = 2
LHS = 4 (sin4 30° + cos4 60°) – 3 (cos2 45° – sin2 90°)
= 4[(½)4 + (½)4] – 3 [(1/√2)2 – 12]
= 4[½ × ½ × ½ × ½ + ½ × ½ × ½ × ½] – 3 [½ – 1]
= 4 [1/16 + 1/16] – 3 (- ½)
= 4[(1 + 1)/16] + 3/2
= (4 × 3)/16 + 3/2
= 8/16 + 3/2
= ½ + 3/2
= (1 + 3)/2
= 4/2
= 2
= RHS
Hence, LHS = RHS.
(iii) cos 60° = cos2 30° – sin2 30°
LHS = cos 60° = ½
RHS = cos2 30° – sin2 30°
= (√3/2)2 + (1/2)2
= ¾ – ¼
= (3 – 1)/4
= 2/4
= ½
= RHS
Hence, LHS = RHS.
(ML Aggarwal Trigonometrical Ratios of Standards Angles Exe-18.1 Class 9)
Question 5.
(i) If x = 30°, verify that tan 2x = 2tanx/ (1- tan2 x).
(ii) If x = 15°, verify that 4 sin 2x cos 4x sin 6x = 1.
Answer :
(i) x = 30°
Consider LHS = tan 2x
Substituting the value of x
= tan 60°
= √3
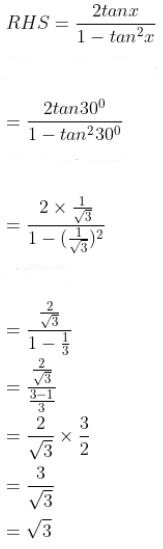
Hence, LHS = RHS.
(ii) x = 15°
2x = 15 × 2 = 30°
4x = 15 × 4 = 60°
6x = 15 × 6 = 90°
LHS = 4 sin 2x cos 4x sin 6x
= 4 sin 30° cos 60° sin 90°
= 4 × ½ × ½ × 1
= 1
= RHS
Hence, LHS = RHS.
Question 6. Find the values of:
……………….
Answer :
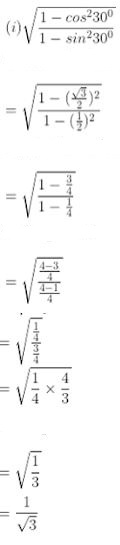
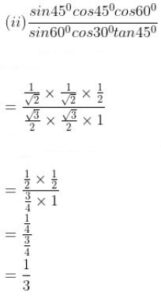
Question 7. If θ = 30°, verify that
(i) sin 2θ = 2 sin θ cos θ
(ii) cos 2θ = 2 cos2 θ – 1
(iii) sin 3θ = 3 sin θ – 4 sin3 θ
(iv) cos 3θ = 4 cos3 θ – 3 cos θ.
Answer :
θ = 30°
(i) sin 2θ = 2 sin θ cos θ
LHS = sin 2θ
= sin 2 × 30°
= sin 60°
= √3/2
RHS = 2 sin θ cos θ
= 2 sin 30° cos 30°
= 2 × ½ × √3/2
= 1 × √3/2
= √3/2
Hence, LHS = RHS.
(ii) cos 2θ = 2 cos2θ – 1
LHS = cos 2θ
= cos 2 × 30°
= cos 60°
= ½
RHS = 2 cos2 θ – 1
= 2 cos2 30° – 1
= 2 (√3/2)2 – 1
= 2 × ¾ – 1
= 3/2 – 1
= (3 – 2)/2
= ½
Hence, LHS = RHS.
(iii) sin 3θ = 3 sin θ – 4 sin3 θ
Consider
LHS = sin 3θ
= sin 3 × 30°
= sin 90°
= 1
RHS = 3 sin θ – 4 sin3 θ
= 3 sin 30° – 4 sin3 30°
= (3×½) – 4×(1/2)3
= 3/2 – 4× 1/8
= 3/2 – ½
Taking LCM
= (3 – 1)/2
= 2/2
= 1
Hence, LHS = RHS.
(iv) cos 3θ = 4 cos3 θ – 3 cos θ
LHS = cos 3θ
= cos 3 × 30°
= cos 90°
= 0
RHS = 4 cos3 θ – 3 cos θ
= 4 cos3 30° – 3 cos 30°
= 4×(√3/2)3 – 3×(√3/2)
= 4× 3√3/8 – 3√3/2
= 3√3/2 – 3√3/2
= 0
Hence, LHS = RHS.
(ML Aggarwal Trigonometrical Ratios of Standards Angles Exe-18.1 Class 9)
Question 8. If 0 = 30°, find the ratio 2 sin 0: sin 2 0.
Answer :
θ = 30°
2 sin θ: sin 2θ = 2sin 30°: sin(2×30°)
= 2 sin 30°: sin 60°
= 2 sin 30°/sin 60°
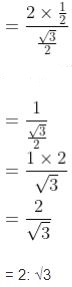
Hence,
2 sin θ: sin 2θ = 2: √3.
Question 9. By means of an example, show that sin (A + B) ≠ sin A + sin B.
Answer :
A = 30° and B = 60°
LHS = sin (A + B)
= sin (30° + 60°)
= sin 90°
= 1
RHS = sin A + sin B
= sin 30° + sin 60°
= ½ + √3/2
= (1 + √3)/2
Hence, LHS ≠ RHS i.e. sin (A + B) ≠ sin A + sin B.
Question 10. If A = 60° and B = 30°, verify that
(i) sin (A + B) = sin A cos B + cos A sin B
(ii) cos (A + B) = cos A cos B – sin A sin B
(iii) sin (A – B) = sin A cos B – cos A sin B
(iv) tan (A – B) = (tan A – tan B)/ (1 + tan A tan B).
Answer :
A = 60° and B = 30°
(i) sin (A + B) = sin A cos B + cos A sin B
Here
LHS = sin (A + B)
= sin (60° + 30°)
= sin 90°
= 1
RHS = sin A cos B + cos A sin B
= sin 60° cos 30° + cos 60° sin 30°
= (√3/2 × √3/2) + (½ × ½)
= ¾ + ¼
= 4/4
= 1
Hence, LHS = RHS.
(ii) cos (A + B) = cos A cos B – sin A sin B
Here
LHS = cos (A + B)
= cos (60° + 30°)
= cos 90°
= 0
RHS = cos A cos B – sin A sin B
= cos 60° cos 30° – sin 60° sin 30°
= (½× √3/2) – √3/2 + ½
= √3/4 – √3/4
= 0
Hence, LHS = RHS.
(iii) sin (A – B) = sin A cos B – cos A sin B
Here
LHS = sin (A – B)
= sin (60° – 30°)
= sin 30°
= ½
RHS = sin A cos B – cos A sin B
= sin 60° cos 30° – cos 60° sin 30°
= (√3/2 × √3/2) – (½ × ½)
= ¾ – ¼
= (3 – 1)/ 4
= 2/4
= ½
Hence, LHS = RHS.
(iv) tan (A – B) = (tan A – tan B)/ (1 + tan A tan B)
Here
LHS = tan (A – B)
= tan (60° – 30°)
= tan 30°
= 1/√3
RHS = (tan A – tan B)/ (1 + tan A tan B)
= (tan 60° – tan 30°)/(1 + tan 60° tan 30°)
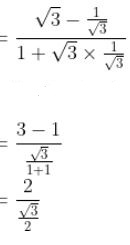
= 2/√3 × ½
= 1/√3
Hence, LHS = RHS.
(ML Aggarwal Trigonometrical Ratios of Standards Angles Exe-18.1 Class 9)
Question 11.
(i) If 2θ is an acute angle and 2 sin 2θ = √3, find the value of θ.
(ii) If 20° + x is an acute angle and cos (20° + x) = sin 60°, then find the value of x.
(iii) If 3 sin2 θ = 2 ¼ and θ is less than 90°, find the value of θ.
Answer :
(i) 2θ is an acute angle
2 sin 2θ = √3
sin 2θ = √3/2 = sin 60°
2θ = 60°
θ = 60°/2 = 30°
Hence, θ = 30°
(ii) 20° + x is an acute angle
cos (20° + x) = sin 60°
cos (20° + x) = sin 60° = cos (90° – 60°)
= cos 30°
20° + x = 30°
⇒ x = 30° – 20° = 10°
Hence, x = 100.
(iii) 3 sin2 θ = 2 ¼
θ is less than 90°
sin2 θ = 9/(4 × 3) = ¾
sin θ = √3/2 = sin 60°
θ = 60°
Hence, θ = 60°.
Question 12. If θ is an acute angle and sin θ = cos θ, find the value of θ and hence, find the value of 2 tan2 θ + sin2 θ – 1.
Answer :
sin θ = cos θ
sin θ/cos θ = 1
tan θ = 1
tan 45° = 1
tan θ = tan 45°
θ = 45°
2 tan2 θ + sin2 θ – 1 = 2 tan2 45° + sin2 45° – 1
= 2 (1)2 + (1/√2)2 – 1
= (2×1×1) + ½ – 1
= 2 + ½ – 1
= 5/2 – 1
= (5 – 2)/2
= 3/2
Hence, 2 tan2 θ + sin2 θ – 1 = 3/2.
Question 13. From the adjoining figure, find
(i) tan x°
(ii) x
(iii) cos x°
(iv) use sin x° to find y.
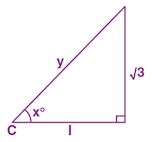
Answer :
(i) tan x° = perpendicular/base
= AB/BC
= √3/1
= √3
(ii) tan x° = √3
tan 60° = √3
tan x° = tan 60°
x = 60
(iii) cos x° = cos 60°
cos x° = ½
(iv) sin x° = perpendicular/hypotenuse = AB/AC
Substitute x = 60 from (ii)
sin 60° = √3/y
sin 60° = √3/2
√3/2 = √3/y
y = (√3×2)/√3
y = (2×1)/1 = 2
Hence, y = 2.
Question 14. If 3θ is an acute angle, solve the following equations for θ:
(i) 2 sin 3θ = √3
(ii) tan 3θ = 1.
Answer :
(i) 2 sin 3θ = √3
sin 3θ = √3/2
sin 60° = √3/2
sin 3θ = sin 60°
⇒ 3θ = 60°
θ = 60/3 = 20°
(ii) tan 3θ = 1
tan 45° = 1
tan 3θ = tan 45°
3θ = 45°
⇒ θ = 15°
Question 15. If tan 3x = sin 45° cos 45° + sin 30°, find the value of x.
Answer :
tan 3x = sin 45° cos 45° + sin 30°
= (1/√2 × 1/√2) + ½
= ½ + ½
= 1
tan 3x = tan 45°
3x = 45°
x = 45/3 = 15°
Hence, the value of x is 15°.
Question 16. If 4 cos2 x° – 1 = 0 and 0 ≤ x ≤ 90, find
(i) x
(ii) sin2 x° + cos2 x°
(iii) cos2 x° – sin2 x°
Answer :
4 cos2 x° – 1 = 0
⇒ 4cos2 x° = 1
cos2 x° = ¼
⇒ cos x° = ± √1/4
⇒ cos x° = + √1/4 [0 ≤ x ≤ 90°, then cos x° is positive]
⇒ cos x° = ½
cos 60° = ½
cos x° = cos 60°
x = 60
(ii) sin2 x° + cos2 x° = sin2 60° + cos2 60°
= (√3/2)2 + (1/2)2
= ¾ + ¼
= (3 + 1)/4
= 4/4
= 1
Hence, sin2 x° + cos2 x° = 1.
(iii) cos2 x° – sin2 x° = cos2 60° – sin2 60°
= (1/2)2 – (√3/2)2
= ¼ – (√3/2 × √3/2)
= ¼ – ¾
= (1 – 3)/4
= -2/4
= – ½
Hence, cos2 x° – sin2 x° = – ½.
Trigonometrical Ratios of Standards Angles Exercise-18.1
ML Aggarwal Class 9 ICSE Maths Solutions
Page 430
Question 17.
(i) If sec θ = cosec θ and 0° ≤ θ ≤ 90°, find the value of θ.
(ii) If tan θ = cot θ and 0° ≤ θ ≤ 90°, find the value of θ
Answer :
(i) sec θ = cosec θ
sec θ = 1/cos θ
cosec θ = 1/sin θ
1/cos θ = 1/sin θ
⇒ sin θ/cos θ = 1
⇒ tan θ = 1
Here tan 45° = 1
tan θ = tan 45°
θ = 45°
(ii) tan θ = cot θ
cot θ = 1/tan θ
tan θ = 1/tan θ
tan2 θ = 1
⇒ tan θ = ± √1
⇒ tan θ = + 1 [0 ≤ θ ≤ 90°, tan θ is positive]
⇒ tan θ = tan 45°
θ = 45°
Question 18. If sin 3x = 1 and 0° ≤ 3x ≤ 90°, find the values of
(i) sin x
(ii) cos 2x
(iii) tan2 x – sec2 x.
Answer :
sin 3x = 1
sin 90° = 1
sin 3x = sin 90°
3x = 90
⇒ x = 90/3
⇒ x = 30°
(i) sin x = sin 30° = 1/2
(ii) cos 2x = cos 2 × 30 = cos 60° = 1/2
(iii) tan2 x – sec2 x = tan2 30° – sec2 30°
= (1/√3)2 – (2/√3)2
= 1/3 – 4/3
= (1 – 4)/3
= – 3/3
= -1
Hence, tan2 x – sec2 x = – 1.
Question 19. If 3 tan2 θ – 1 = 0, find cos 2θ, given that θ is acute.
Answer :
3 tan2 θ – 1 = 0
3 tan2 θ = 1
⇒ tan2 θ = 1/3
⇒ tan θ = 1/√3 [θ is acute so tan θ is positive]
θ = 30°
cos 2θ = cos 2 × 30°
= cos 60° = ½
Question 21. If sin x + cos y = 1, x = 30° and y is acute angle, find the value of y.
Answer :
sin x + cos y = 1
x = 30°
sin 30° + cos y = 1
⇒ 1/2 + cos y = 1
cos y = 1 – ½
cos y = (2 – 1)/2 = ½
cos 60° = ½
cos y = cos 60°
y = 60°
(ML Aggarwal Trigonometrical Ratios of Standards Angles Exe-18.1 Class 9)
Question 21. If sin (A + B) = √3/2 = cos (A – B), 0° < A + B ≤ 90° (A > B), find the values of A and B.
Answer :
sin (A + B) = √3/2 = cos (A – B)
sin (A + B) = √3/2
sin 60 = √3/2
sin (A + B) = sin 60°
A + B = 60° …(1)
cos (A – B) = √3/2
cos 30° = √3/2
cos (A – B) = cos 30°
A – B = 30° …(2)
By adding both the equations
A + B + A – B = 60° + 30°
2A = 90°
⇒ A = 90°/2 = 45°
Now substitute the value of A in equation (1)
45° + B = 60°
B = 60° – 45° = 15°
Hence, A = 45° and B = 15°.
Question 22. If the length of each side of a rhombus is 8 cm and its one angle is 60°, then find the lengths of the diagonals of the rhombus.
Answer :
Each side of a rhombus = 8 cm
One angle = 60°
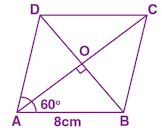
∠OAB = 60°/2 = 30°
In right ∠AOB
sin 30° = OB/AB
½ = OB/8
OB = 8/2 = 4 cm
BD = 2OB = 2 × 4 = 8 cm
cos 30° = AO/AB
√3/2 = AO/8
AO = 8√3/2 = 4√3
AC = 4√3 × 2 = 8 √3 cm
Hence,
The length of the diagonals of the rhombus are 8 cm and 8√3 cm.
Question 23. In the right-angled triangle ABC, ∠C = 90° and ∠B = 60°. If AC = 6 cm, find the lengths of the sides BC and AB.
Answer :
In the right-angled triangle ABC, ∠C = 90° and ∠B = 60°
AC = 6 cm
tan B = AC/BC
tan 60° = 6/BC
So we get
√3 = 6/BC
⇒ BC = 6/√3
= 6√3/(√3+√3)
= 6√3/3
= 2√3 cm
sin 60° = AC/AB
√3/2 = 6/AB
AB = (6×2)/√3
AB = (12×√3)/(√3×√3)
= 12√3/3
= 4√3 cm
Hence,
the lengths of the sides BC = 2√3 cm and AB = 4√3 cm.
Question 24. In the adjoining figure, AP is a man of height 1.8 m and BQ is a building 13.8 m high. If the man sees the top of the building by focusing his binoculars at an angle of 30° to the horizontal, find the distance of the man from the building.
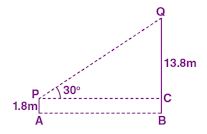
Answer :
Height of man AP = 1.8 m
Height of building BQ = 13.8 m
Angle of elevation from the top of the building to the man = 30°
AB = x then PC = x
QC = 13.8 – 1.8 = 12 m
In right △ PQC
tan θ = QC/PC
tan 30° = 12/x
1/√3 = 12/x
x = 12 √3 m
Hence,
the distance of the man from the building is 12 √3 m.
(ML Aggarwal Trigonometrical Ratios of Standards Angles Exe-18.1 Class 9)
Question 25. In the adjoining figure, ABC is a triangle in which ∠B = 45° and ∠C = 60°. If AD ⟂ BC and BC = 8 m, find the length of the altitude AD.
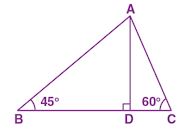
Answer :
ABC
∠B = 45° and ∠C = 60°
AD ⟂ BC and BC = 8 m
In right △ ABD
tan 45° = AD/BD
1 = AD/BD
AD = BD
In right △ ACD
tan 60° = AD/DC
√3 = AD/DC
⇒ DC = AD/√3
BD + DC = AD + AD/√3
BC = (√3AD + AD)/ √3
⇒ 8 = [AD (√3 + 1)]/ √3
AD = 8√3/(√3 + 1)
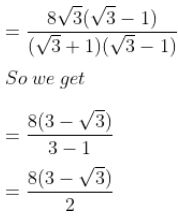
= 4 (3 – √3) m
— : End of ML Aggarwal Trigonometrical Ratios of Standards Angles Exe-18.1 Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends




