ML Aggarwal Circle Exe-15.1 Class 9 ICSE Maths APC Understanding Solutions. Solutions of Exe-15.1. This post is the Solutions of ML Aggarwal Chapter 15 – Circle for ICSE Maths Class-9. APC Understanding ML Aggarwal Solutions (APC) Avichal Publication Solutions of Chapter-15 Circle for ICSE Board Class-9. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Circle Exe-15.1 Class 9 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 9th |
| Chapter-15 | Circle |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-15.1 Questions |
| Edition | 2021-2022 |
Exe-15.1 Solutions of ML Aggarwal for ICSE Class-9 Ch-15, Circle
Note:- Before viewing Solutions of Chapter -15 Circle Class-9 of ML Aggarwal Solutions . Read the Chapter Carefully. Then solve all example given in Exercise-15.1, Exe-15.2, MCQs, Chapter Test.
Circle Exercise-15.1
ML Aggarwal Class 9 ICSE Maths Solutions
Page 335
Question 1. Calculate the length of a chord which is at a distance of 12 cm from the centre of a circle of radius 13 cm.
Answer :
AB is chord of a circle with center O and OA is its radius OM ⊥ AB
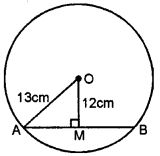
Hence, OA = 13 cm, OM = 12 cm
Now from right angled triangle OAM,
OA2 = OM2 + AM2
⇒ 132 = 122 + AM2
⇒ AM2 = 132 – 122
⇒ AM2 = 169 – 144
⇒ AM2 = 25
⇒ AM2 = 52
⇒ AM = 5
OM perpendicular to AB
Hence, M is the midpoint of AB
AB = 2 AM
⇒ AB = 2 (5)
⇒ AB = 10 cm
Question 2. A chord of length 48 cm is drawn in a circle of radius 25 cm. Calculate its distance from the centre of the circle.
Answer :
AB is the chord of the circle with centre O and radius OA
OM is perpendicular to AB
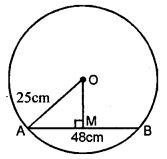
Hence, AB = 48 cm
OA = 25 cm
OM ⊥ AB
M is the mid-point of AB
AM = 1/2 AB = ½ × 48 = 24 cm
Now right ∆OAM,
OA2 = OM2 + AM2
⇒ (25)2 = OM 2 + (24)2
⇒ OM2 = (25)2 – (24)2 = 625 – 576
⇒ OM2 = 49 = (7)2
⇒ OM = 7 cm
Question 3. A chord of length 8 cm is at a distance of 3 cm from the centre of the circle. Calculate the radius of the circle.
Answer :
AB is the chord of a circle with center O
And radius OA and OM ⊥ AB
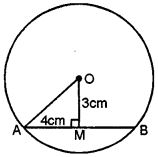
AB = 8 cm
OM = 3 cm
OM ⊥ AB
M is the mid-point of AB
AM = ½ AB = ½ × 8 = 4 cm.
Now in right ∆OAM
OA2 = OM2 + AM2
= (3)2 + (4)2 = 9 + 16 = 25
= (5)2
⇒ OA = 5 cm.
Question 4. Calculate the length of the chord which is at a distance of 6 cm from the centre of a circle of diameter 20 cm.
Answer :
AB is the chord of the circle with centre O
And radius OA and OM ⊥ AB
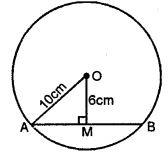
Diameter of the circle = 20 cm
Radius = 20/2 = 10 cm
OA = 10 cm, OM = 6 cm
Now in right ∆OAM,
OA2 = AM2 + OM2
⇒ (10)2 = AM2 + (6)2
⇒ AM2 = 102 – 62
⇒ AM2 = 100 – 36 = 64 = (8)2
⇒ AM = 8 cm
OM ⊥ AB
M is the mid-point of AB.
⇒ AB = 2× AM = 2×8 = 16 cm.
Question 5. A chord of length 16 cm is at a distance of 6 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 8 cm from the centre.
Answer :
AB is a chord a circle with centre O and
OA is the radius of the circle and OM ⊥ AB
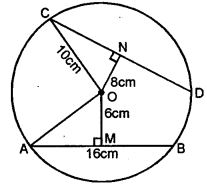
AB = 16 cm, OM = 6 cm
OM ⊥ AB
AM = ½ AB = ½ × 16 = 8 cm
Now in right ∆OAM
OA2 = AM2 + OM2
= (8)2 + (6)2
⇒ 64 + 36 = 100 = (10)2
ON ⊥ CD and OC is the radius.
In right ∆ONC
OC2 = ON2 + NC2
⇒ (10)2 = (8)2 + (NC)2
⇒ 100 = 64 + NC2
⇒ NC 2 = 100 – 64 = 36 = (6)2
⇒ NC = 6
But ON ⊥ AB
N is the mid-point of CD
⇒ CD = 2 NC
= 2×6 = 12 cm
Question 6. In a circle of radius 5 cm, AB and CD are two parallel chords of length 8 cm and 6 cm respectively. Calculate the distance between the chords if they are on :
(i) the same side of the centre.
(ii) the opposite sides of the centre
Answer :
Two chords AB and CD of a Circle with centre O and radius OA or OC
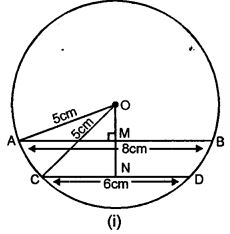
OA = OC = 5 cm
AB = 8 cm
CD = 6 cm
OM and ON are perpendiculars from O to AB and CD respectively.
M and N are the Mid-points of AB and
CD respectively
In figure (i) chord are on the same side
And in figure (ii) chord are on the opposite
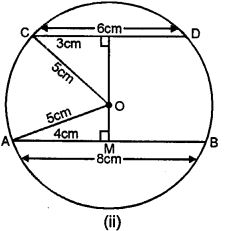
OA2 = AM2 + OM2
⇒ (5)2 = (4)2 + OM2
⇒ AM = ½ AB
⇒ 25 = 16 + OM2
⇒ OM2 = 25 – 16 = 9= (3)2
⇒ OM = 3 cm
Again in right ∆OCN,
OC2 = CN2 + ON2
⇒ (5)2 = (3)2 + ON2
⇒ (CN = ½ CD)
⇒ 25 = 9 + ON2
⇒ ON2 = 25 – 9 = 16 = (4)2
⇒ ON = 4
In fig (i), distance MN = ON – OM
= 4 – 3 = 1cm.
In fig (ii)
MN = OM + ON
= 3 + 4
= 7 Cm
Question 7. (a) In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle, OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the:
(i) radius of the circle.
(ii) length of chord CD.
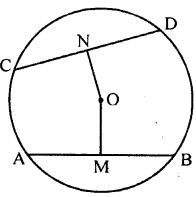
(b) In the figure (ii) given below, CD is the diameter which meets the chord AB in E such that AE = BE = 4 cm. If CE = 3 cm, find the radius of the circle.
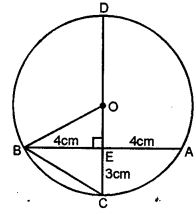
Answer :
(a) AB = 24 cm, OM = 5cm, ON = 12cm
OM ⊥ AB
M is midpoint of AB
AM = 12 cm
(i) Radius of circle OA = √OM2 + AM2
(ii) Again OC2 = ON2 + CN2
⇒ 132 = 122 + CN2
⇒ CN = √(132 – 122)
= √(169 – 144)
= √25
⇒ CN = 5 cm

As ON ⊥ CD, N is mid-Point of CD
CD = 2CN
= 2×5
= 10 cm
(b) AB = 8 cm,
EC = 3 cm
Let radius OB = OC = r
OE = (r-3) cm
Now in right ∆OBE
OB2 = BE2 + OE2
⇒ r2 = (4)2 + (r – 3)2
⇒ r2 = 16 + r2 – 6r + 9
⇒ 6r = 25
⇒ r = 25/6
= 4 1/6 cm
Question 8. In the adjoining figure, AB and CD ate two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
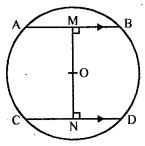
Answer :
In the figure, chords AB ∥ CD
O is the centre of the circle
Radius of the Circle = 15 cm
Length of AB = 24 cm and CD = 18 cm
Join OA and OC

AB = 24 cm and OM ⊥ AB
AM = MB = 24/2
= 12 cm
ON ⊥ CD
CN = ND = 18/2 = 9 cm
Similarly In right ∆ CNO
OC2 = CN2 + ON2 (15)2
= (9)2 + ON2
⇒ 225 = 81 + ON2
⇒ ON2 = 225 – 81
= 144 = (12)2
⇒ ON = 12 cm
Now MN = OM + ON
= 9 + 12
= 21 cm
Question 9. AB and CD are two parallel chords of a circle of lengths 10 cm and 4 cm respectively. If the chords lie on the same side of the centre and the distance between them is 3 cm, find the diameter of the circle.
Answer :
AB and CD are two parallel chords and AB = 10 cm, CD = 4 cm and distance between
AB and CD = 3 cm
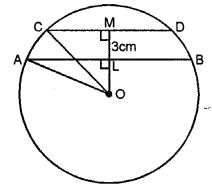
circle OA = OC = r
OM ⊥ CD which intersects AB in L.
OL = x, then OM = x + 3
OA2 = AL2 + OL2
⇒ r2 = (5)2 + x2
= 25 + x2
Again in right ∆OCM
OC2 = CM2 + OM2
⇒ r2 = (2)2 + (x + 3)2
⇒ r2 = 4 + (x + 3)2
⇒ r2 = 4 + (x + 3)2
from (i) and (ii)
25 + x2 = 4 + (x + 3)2
⇒ 25 + x2
= 4 + x2 + 9 + 6x
⇒ 6x = 25 – 13
= 12
⇒ x = 12/6
= 2 cm
Substituting the value of x in (i)
r2 = 25 + x2 = 25 + (2)2
= 25 + 4
⇒ r2 = 29
⇒ r = √29cm
Diameter of the circle = 2 r
= 2 ×√29 cm
= 2√29 cm
Question 10. ABC is an isosceles triangle inscribed in a circle. If AB = AC = 12√5 cm and BC = 24 cm, find the radius of the circle.
Answer :
AB = AC 12√5 and
BC = 24 cm
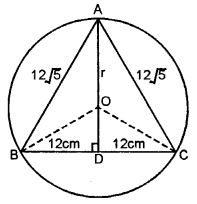
Join OB and OC and OA
Draw AD ⊥ BC which will pass through
OD bisect BC in D
BD = DC = 12 cm
In right ∆ABD
AB2 = AD2 + BD2
⇒ (12√5)2 = AD2 + BD2
⇒ (12√5)2 = AD2 + (12)2
⇒ 144×5 =AD2 + 144
⇒ 720 – 144
= AD2
⇒ AD2 = 576
⇒ AD = √576
= 24
Let radius of the circle = OA = OB = OC = r
OD = AD – AO = 24 – r
Now in right ∆OBD,
OB2 = BD2 + OD2
⇒ r2 = (12)2 + (24 – r)2
⇒ r2 = 144 + 576 + r2 – 48r
⇒ 48r = 720
⇒ 48r = 720
⇒ r = 720/48
= 48r
⇒ 48r = 720
⇒ r = 720/48
= 15cm.
Radius = 15 cm.
Question 11. An equilateral triangle of side 6 cm is inscribed in a circle. Find the radius of the circle.
Answer :
ABC is an equilateral triangle inscribed in a
Circle with centre O. Join OB and OC,
From A, Draw AD ⊥ BC which will pass
Through the centre O of the circle.
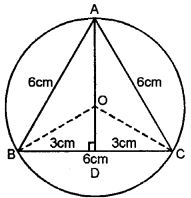
Each side of ∆ABC = 6 cm.
AD = √3/2 a= √3/2 × 6 = 3 √3 cm.
OD = AD – AO = 3√3 – r
Now in right ∆OBD
OB2 = BD2 + OD2
⇒ r2 = (3)2 + (3√3-r)2
⇒ r2 = 9 + 27 + r2 -6√3r
⇒ 6√3r = 36
⇒ R = 36/6√3
= 6/√3 × √3/√3
= 6√3/3
= 2√3 cm
Radius = 2√3 cm
Question 12. AB is a diameter of a circle. M is a point in AB such that AM = 18 cm and MB = 8 cm. Find the length of the shortest chord through M.
Answer :
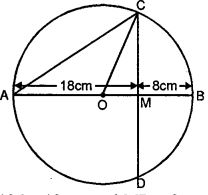
AM = 18 cm and MB = 8 cm
AB = AM + MB = 18 + 8
= 26 cm
Radius of the circle = 26/2
= 13 cm
Let CD is the shortest chord drawn through M.
CD ⊥ AB
Join OC
OM = AM – AO
= 18 – 13
= 5 cm
OC = OA = 13 cm
Now in right ∆OMC
OC2 = OM2 + MC2
⇒ (13)2 = (5)2 + MC2 (MC2
= 132 – 52
⇒ MC2 = 169 – 25
= 144 = (12)2
⇒ MC = 12
M is Mid-Point of CD
CD = 2 ×MC
= 2×12
= 24 cm
Question 13. A rectangle with one side of length 4 cm is inscribed in a circle of diameter 5 cm. Find the area of the rectangle.
Answer :
Here, Diameter of rectangle = Diagonal of rectangle = 5 cm
Circle Exercise-15.1
ML Aggarwal Class 9 ICSE Maths Solutions
Page 336
Question 14. The length of the common chord of two intersecting circles is 30 cm. If the radii of the two circles are 25 cm and 17 cm, find the distance between their centres.
Answer :
Let the circles with centres A and B intersect each other at C and D.
RA = 25 cm, RB = 17 cm, CD = 30 cm.
Let CD and AB intersect at O.
OC=OD = 30/2 = 15 cm.
AO = [RA2-OC2]0.5 = [252–152]0.5
= [625–225]0.5 = 20 cm.
BO = [RB2-OC2]0.5 = [172–152]0.5
= [289–225]0.5 = 8 cm.
Hence AB = 20+8 = 28 cm.
Question 15. The line joining the mid-points of two chords of a circle passes through its centre. Prove that the chords are parallel.
Answer :
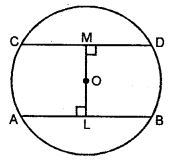
AB and CD are the two chords of a circle with centre O.
L and M are the midpoints of AB and CD and O lies in the line joining ML
To prove: AB ∥ CD
Proof: AB and CD are two chords of a circle with centre O.
Line LOM bisects them at L and M
Then, OL ⊥ AB
And, OM ⊥ CD
∴ ∠ALM = ∠LMD = 90°
But they are alternate angles
∴ AB ∥ CD.
Question 16. If a diameter of a circle is perpendicular to one of two parallel chords of the circle, prove that it is perpendicular to the other and bisects it.
Answer :
Draw the figure
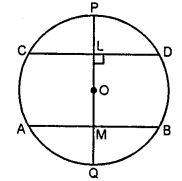
Chord AB || CD
The diameter PQ is perpendicular to AB.
To prove:
PQ is perpendicular to CD.
Proof:
Let diameter PQ ⊥ AB
∴∠AMO = 90⁰
It is given that AB || CD
∴ ∠AMO = ∠OLD = 90⁰
Hence OL ⊥ CD
∴ PQ ⊥ CD
PQ bisects CD as perpendicular to the chord from the center of the circle bisects the chord.
Hence proved.
Question 17. In an equilateral triangle, prove that the centroid and the circumcentre of the triangle coincide.
Answer :
An equilateral triangle ABC in which D, E and F are the mid- points of sides BC,
CA and AB respectively.
To prove :
The centroid and circumcentre are coincident.
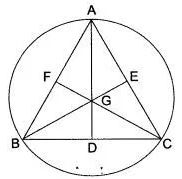
Draw medians, AD, BE and CF.
Proof :
Let G be the centroid of ΔABC i. e., the point of intersection of AD, BE and CF. In triangles BEC and BFC, we have
∠B = ∠C = 60
BC = CE [∵ AB = AC ⇒ ½ AB = ½ AC ⇒ BF = CE]
∴ ΔBEC ≅ ΔBFC
⇒ BE = CF ……(i)
Similarly, ΔCAF ≅ ΔCAD
CF = AD …….(ii)
From (i) & (ii) AD = BE = CF
⇒ 2/3 AD = 2/3, BE = 2/3 CF
CG = 2/3 CF
GA = 2/3 AD, GB = 2/3 BE
⇒ GA = GB = GC
⇒ G is equidistant from the vertices
⇒ G is the circumcentre of ΔABC
Hence,
the centroid and circumcentre are coincident.
Question 18.
(a) In the figure (i) given below, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA = 2 OD.
(b) In the figure (ii) given below, O is the centre of a circle. If AB and AC are chords of the circle such that AB = AC and OP ⊥ AB, OQ ⊥ AC, Prove that PB = QC.
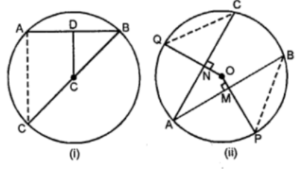
Answer :
(a) Since, OD ⊥ AB and the perpendicular drawn from the centre to a chord bisects the chord.
∴ D is the mid-point of AB.
Also, O being the centre , is the mid – point of BC.
Thus, in ΔABC, D and O are mid-point of AB and BC respectively. Therefore, OD ∥ AC
And OD = ½ CA [∵ Segment joining the mid- points of two sides of a triangle is half of the third side]
⇒ CA = 2OD.
Hence proved.
(b) AB and AC are two equal chords of a circle with centre O.
OP⊥AB and OQ⊥AC.
To prove: PB=QC
Proof:
OP⊥AB
⇒AM=MB …. (perpendicular from centre bisects the chord)….(i)
Similarly, AN=NC….(ii)
But, AB=AC
⇒ 2AB = 2AC
⇒ MB = NC …(iii) ( From (i) and (ii) )
OP=OQ (Radii of the circle)
and OM=ON (Equal chords are equidistant from the centre)
⇒ OP − OM = OQ − ON
⇒ MP = NQ ….(iv) (From figure)
In ΔMPB and ΔNQC, we have
∠PMB = ∠QNC (Each =90∘)
MB = NC ( From (iii) )
MP = NQ ( From (iv) )
∴ ΔPMB ≅ ΔQNC (SAS)
⇒ PB = QC (CPCT)
Question 19.
(a) In the figure (i) given below, a line l intersects two concentric circles at the points A, B, C and D. Prove that AB = CD.
(b) In the figure (it) given below, chords AB and CD of a circle with centre O intersect at E. If OE bisects ∠AED, Prove that AB = CD.
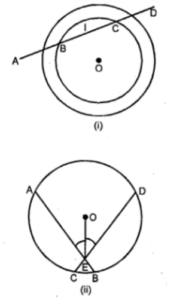
Answer :
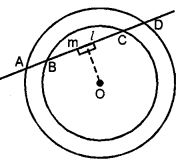
(a) Since, perpendicular from the centre to a chord bisects the chord, therefore,
AM = MD …(i)
and BM = MC …(ii)
(i) and (ii) gives, AM – BM = MD – MC
⇒ AB = CD.
(b)
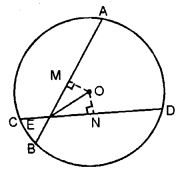
Draw OM⊥AB and ON⊥CD.
In △OEM and △OEN,
∠OME = ∠ONE=90o
∠OEM = ∠OEN
OE = OE
Hence,
by AAS congruence,
△OEM ≅ △OEN
So, OM=ON [By cpct ]
Chords AB and CD are equidistant from the centre.
So,
Chord AB = Chord CD
Question 20.
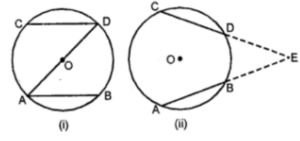
(a) In the figure (i) given below, AD is a diameter of a circle with centre O.
If AB || CD, prove that AB = CD.
(b) In the figure (ii) given below, AB and CD are equal chords of a circle with centre O. If AB and CD meet at E (outside the circle) Prove that :
(i) AE = CE (ii) BE = DE.
Answer :
(a) We can join
in triangles ABO and DOC,
BO = OD (Radius)
Ang. BOA = Ang. DOC (Vertically opp angle)
AO= OC (Radius)
By SAS, ABO is congruent to DOC.
By CPCT, AB = CD
Hence proved
(b)
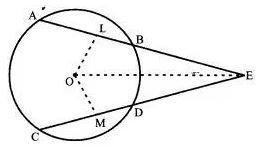
Two equal chords AB and CD intersecting at a point E.
To prove :
BE = DE and AE = CE
Join OE. Draw OL ⊥ AB and OM ⊥ CD.
Proof :
AB = CD
⇒ OL = OM [∵ Equal chords are equidistant from the centre ]
In triangles OLE and OME, we have
OL = OM
∠OLE = ∠OME [Each equal to 90˚]
OE = OE [Common]
So,
by SAS – criterion of congruences
△OLE ≅ △OME
⇒ LE = ME ……..(i)
Now, AB = CD
⇒ ½ AB = ½ CD ⇒ BL = DM …….(ii)
Subtracting (ii) from (i), we get
LE – BL = ME – DM
⇒ BE = DE
AB = CD and BE = DE
⇒ AB + BE = CD + DE
⇒ AE = CE
Hence,
BE = DE and AE = CE
Hence proved.
— : End of ML Aggarwal Circle Exe-15.1 Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends




